Gases and Gas laws (Ideal gases) | Conceptual notes | Complete solutions to short questions and numerical problems | Grade 11 (Physics) | Physics in Depth

Gases and Gas Laws

• The thermal expansion of gas is very large compared to those of solids and liquids.



• To state the condition of a gas, its temperature, pressure and volume are required.



• The relationship between temperature, pressure and volume of a gas can be expressed in very simple laws, called the Gas laws and reduced to a simple equation called the equation of state ( PV = nRT ).



• Dalton's law of partial pressure : It states that total pressure exerted by a mixture of gases is equal to the sum of the partial pressure of the individual gas when there is no chemical interaction between them . If \(p_1\) and \(p_2\) are the pressure exerted by the gas '1' and gas '2' when mixed, then the total pressure of the mixture is \[p=p_1+p_2\]



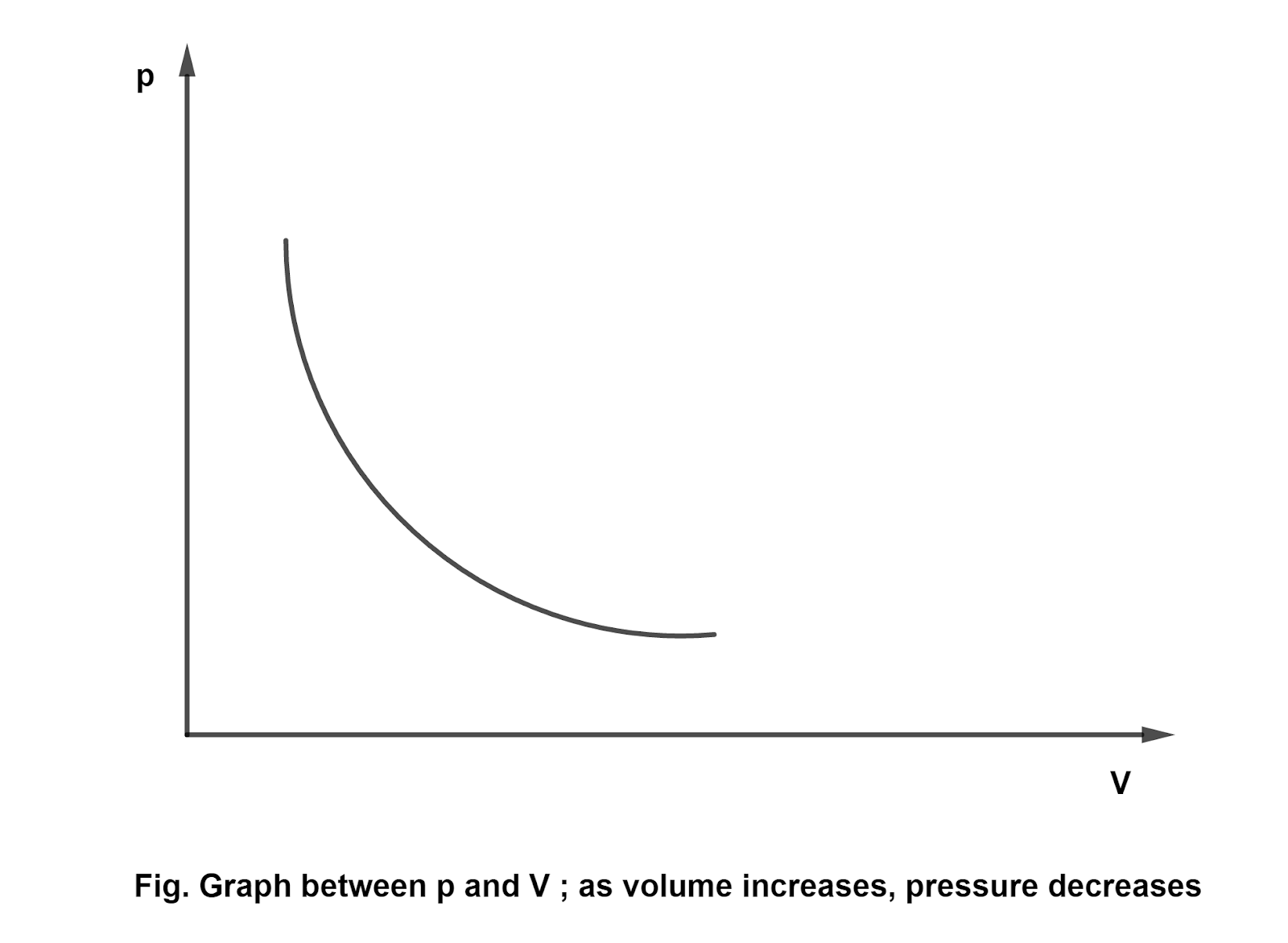
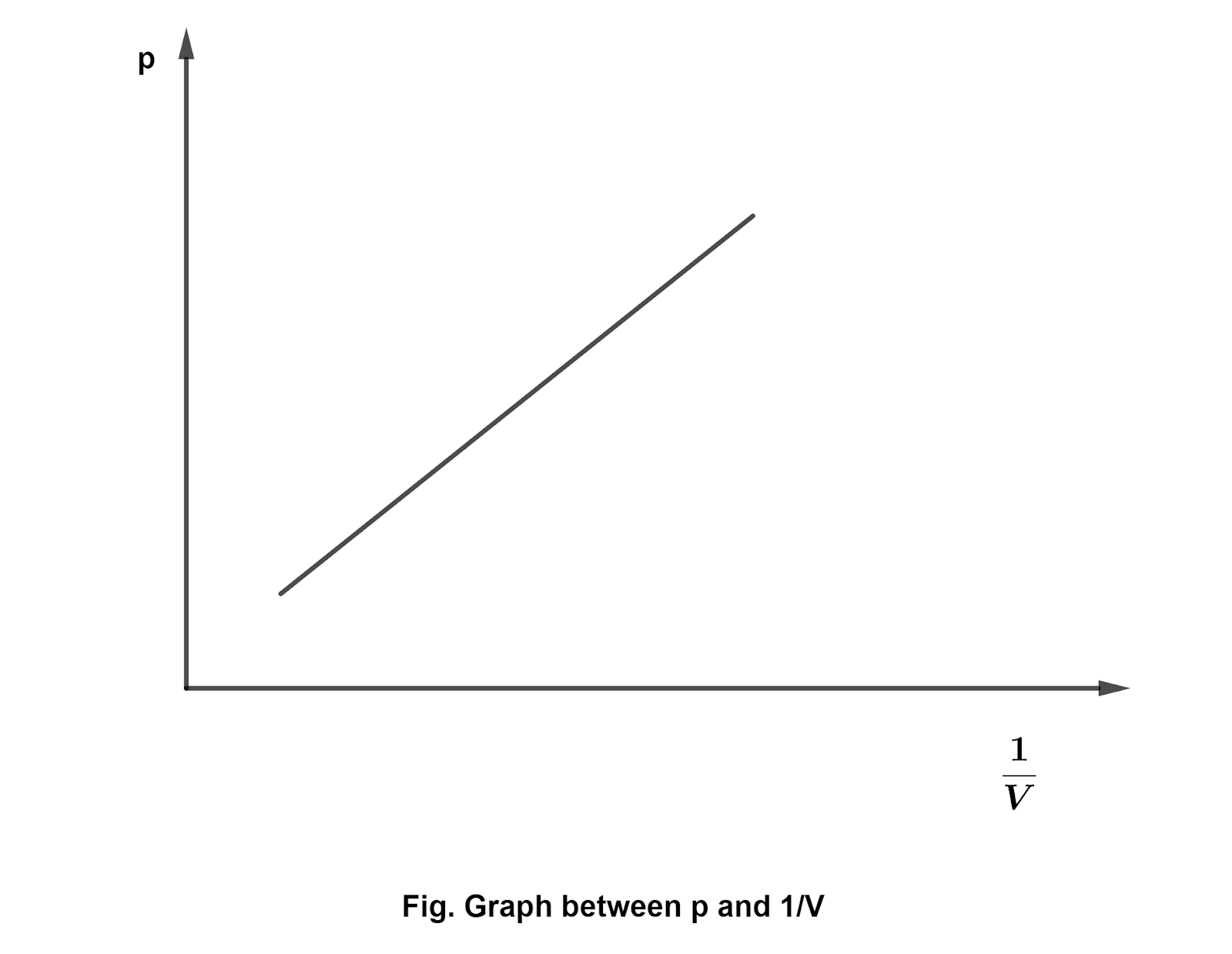
• Boyle's law : It states that, On temperature keeping constant, the volume of the given mass of a gas is inversely proportional to the pressure. i.e., \[p \propto \frac{1}{V}\] \[pV=\text{constant}\] Boyle's law can be depicted through graph as follows:



• Charle's volume law : Charle's volume states that, On pressure keeping constant, the volume of a given mass of the gas is directly proportional to the absolute temperature .
  
  \[V \propto T\]



• Charle's pressure law : Charle's pressure states that, On volume keeping constant, the pressure of the given mass of a gas is directly proportional to the absolute temperature . \[P \propto T\]



• Eqution of state or Ideal gas equation : For n moles of a gas, the equation of state is written as, \[PV=nRT\]



• Universal gas constant, R : It is the amount of work done per mole per unit kelvin. It's value is 8. 31 J mol \(^{-1}\) K\(^{-1}\)



• Gas constant for unit mass, r : \[r=\frac{R}{M}\] Here, M is the molar mass of gas. From the equation of state , \[PV=nRT\] Since, \[n=\frac{m}{M}\] where m is the mass of gas.
  Now, the equation of state can be written as, \[\begin{align*} PV&=\frac{m}{M} R T\\ PV&=m \frac{R}{M} T\\ PV&=m r T \end{align*}\] It's value is 4155 J kg\(^{-1}\) K \(^{-1}\)
.

Short Answer Questions Solution

1. On a chilly morning you can “see your breath.” Can you really? What are you actually seeing? Does this phenomenon depend on the temperature of the air, the humidity, or both? Explain.
   Solution:
   Our lungs are very moist, and every breath we expel is full of water vapor. When the surrounding air is cold, the moisture in the air we breathe out begins to condensate. The droplets are still light enough to float in the air, but they are large enough to be visible. The droplets form more quickly as the temperature drops, and the cloud we see as we breathe out becomes bigger. So, we are seeing our breath and it depends on the temperature and humidity of air.



2. When a car is driven some distance, the air pressure in the tires increases. Why? Should you let out some air to reduce the pressure? Why or why not?
   Solution:
   From the movement of tires and the friction that occur between the tires and the road convert to a heat which increases the temperature of the air inside the tires.
   From Charke's law,
   \[P \propto T\]
   Thus, when the temperature increases, the air pressure in the tires increases.
   It is not good to let some air out to reduce the pressure because the tires will be then under under-inflated when they cool. It is recommended to stop the car and the temperature decreases which will then decrease the pressure.



3. Unwrapped food placed in a freezer experiences dehydration, known as “freezer burn.” Why?
   Solution:
   Freezer burn is the condition which occurs to the food when the air reaches on it. When unwrapped food is placed in the freezer, the ice in the food (water in the food forms the ice crystals) evaporates as the dry air reaches on it. So, as the water from the food is taken off, it looks burnt due to dehydration.



4. A group of students drove from their university (near sea level) up into the mountains for a skiing weekend. Upon arriving at the slopes, they discovered that the bags of potato chips they had brought for snacks had all burst open. What caused this to happen?
   Solution:
   With the increase in altitude, the air pressure decreases. When the students drove to mountains from the sea level, the air pressure is decreased. The potato bags that were sealed at the place with sea level pressure has its own pressure (very high pressure). As they carry it to the mountains, the huge pressure difference between inside and outside of the potato bags cause it to burst.



5. Why fizz comes out when soda bottle is opened?
   Solution:
   Inside the soda bottle, the carbon dioxide is dissolved with the water under very high pressure. When it is opened, there is large pressure difference between inside and outside of the bottle. This results in fizz coming out from the soda bottle to remain in equilibrium by maintaining same pressure within and outside the bottle.



6. Define Boyle's law. Draw necessary graphs.
   Solution:
   Boyles law states that, On temperature keeping constant, the volume of the given mass of a gas is inversely proportional to the pressure. i.e., \[p \propto \frac{1}{V}\] \[pV=\text{constant}\] Boyle's law can be depicted through graph as follows:
   
   



7. On what conditions real gases behave like ideal gases?
   Solution:
   For a gas to behave as an ideal, it must have negligible volume of the molecules and no inter molecular force of attraction between them. It is possible when the pressure is very low such that volume of gas is very large such that the volume of molecules is negligible as compared to the volume of the gas. Similarly, at high temperature, the kinetic energy of the molecules is quite large so that the effect of inter molecular forces on the motion of the molecules is negligible. Hence, at low pressure and high temperature, a real gases behave like ideal gases.

Numerical problem solutions

1. Two bulbs of equal volume are joined by a narrow tube and are filled with a gas at s.t.p. When one bulb is kept in melting ice and the other is placed in a hot bath, the new pressure is 877.6 mm Hg. Calculate the temperature of the bath.
   Solution:
   initial pressure, \(p_1\) = 760 mm Hg (s.t.p.)
   final pressure, \(p_2\) = 877.6 mm Hg
   temperature of a bulb kept in melting ice, \(T_1\) = 273 K
   
   Let V be the volume of each bulb and \(T_2\) be the temperature of hot bath.
   From the relation, \[pV=mrT\] We can write, \[m=\frac{pV}{rT}\] Thus, initial mass of gas in each bulb = \(\frac{p_1V}{r\times 273}\)
   Total mass of air in two bulbs = \(\frac{2p_1V}{r\times 273}\)
   Final mass of gas in cold bulb = \(\frac{p_2 V}{r \times T_1}\)=\(\frac{p_2V}{r \times 273}\)
   Final mass of gas in hot bulb = \(\frac{p_2 V}{r\times T_2}\)
   Since, the total mass remains constant, \[\begin{align*} \text{initial mass}&=\text{final mass}\\ \frac{2p_1V}{r\times 273}&=\frac{p_2 V}{r \times 273}+\frac{p_2 V}{r\times T_2}\\ \frac{2p_1}{273}&=\frac{p_2}{273}+\frac{p_2}{T_2}\\ \frac{2p_1}{273 p_2}&=\frac{1}{273}+\frac{1}{T_2}\\ \left(2\times \frac{760}{877.6}-1\right)\frac{1}{273}&=\frac{1}{T_2}\\ (1.732-1) \times \frac{1}{273}&=\frac{1}{T_2}\\ 0.732 \times T_2&=273\\ T_2&=\frac{273}{0.732}\\ T_2&=372.95 \hspace{0.1cm} \text{K} \end{align*}\]



2. A cylinder of gas has a mass of 10 kg and pressure of 8 atms at 27\(^\circ\) C. When some gas is used in a cold room at -3\(^\circ\) C, the gas remaining in the cylinder at this difference has a pressure of 6.4 atms. Calculate the mass of gas used.
   Solution:
   initial mass, \(m_1\) = 10 kg
   initial temperature, \(T_1\) = 27\(^\circ\) C = 300 K
   final temperature, \(T_2\) = -3 \(^\circ\) C = 273-3 = 270 K
   initial pressure, \(p_1\) = 8 atm
   final pressure, \(p_2\) = 6.4 atm
   final mass, \(m_2\) = ?
   
   Let V be the volume of the cylinder.
   Then,
   \[p_1V=m_1rT_1 ... (i)\] \[p_2 V = m_2 r T_2 ... (ii)\] Dividing eqn (ii) by eqn(i), we get, \[\begin{align*} \frac{p_2}{p_1}&=\frac{m_2}{m_1}\times \frac{T_2}{T_1}\\ m_2&=\frac{p_2}{p_1}\times \frac{T_1}{T_2}\times m_1\\ &=\frac{6.4}{8}\times \frac{300}{270}\times 10\\ &=8.9 \hspace{0.1cm}\text{kg} \end{align*}\] \(\therefore\) The mass of gas used = \(m_1-m_2\) = 10-8.9 = 1.1 kg.