Transfer of heat / Rate of heat flow | Notes | Short answer questions and Numerical problems solutions | Grade 11 NEB (Physics) | Physics in Depth
Transfer of heat
- Heat can be transferred from one place to another by three different methods : Conduction, Convection and Radiation.
- Conduction is the process in which heat is transferred through a material without the movement of material. It usually takes place in solids.
- Convection is the process in which heat is transferred through a substance from one point to another with the actual movement of the heated particles. It takes place in liquids and gases.
- Radiation is the process in which heat is transferred from one place to another directly without heating the intervening medium.
- Thermal conductivity is the measure of ability of a material to conduct heat.
- Coefficient of thermal conduction or Thermal conductivity is expressed as, \[k=\frac{Qx}{A (\theta_2-\theta_1) t}\] Here, k is the thermal conductivity, Q is the quantity of heat flowing through the material, A is the area of the material, t is the time for which the heat flows through the material and \(\theta_2-\theta_1\) is the temperature difference between the two faces of the material.
- A body that absorbs all the radiation falling on it is called a black body . The radiation emitted by a blackbody is called black body radiation. No ideal black body exist. Lamp black is close to a black body. It reflects only about 1 % of the radiation falling on it.
- Emissive power is defined as the energy radiated per unit area per unit time per unit solid angle along the normal to the area. It is mathematically expressed as,
\[e=\int_0 ^ \infty e_\lambda d\lambda\] It's unit is J m\(^{-2}\) s\(^{-1}\) or W m\(^{-2}\).
Here, \(\lambda\) is the wavelength of radiation emitted that ranges from 0 to \(\infty\). - Stefan - Boltzmann law states that the energy of thermal radiation emitted per unit time by a black - body of surface area A is given by,
\[E=\sigma A T^4\]
Where \(\sigma\) is a universal constant known as Stefan - Boltzmann constant and T is its temperature on absolute scale. The measured value of \(\sigma\) is 5.67\(\times\)10\(^{-8}\) W/m\(^2\) - K\(^4\).
A body which is not a black body, emits less radiation given than given by above equation. It is, however, proportional to \(T^4\). The energy emitted by such a body per unit time is written as, \[E=e\sigma A T^4\] Here, e is the emissivity of the surface which has value between 0 and 1.
e = 0 for completely reflecting surface and e = 1 for a black body.
Short Answer Questions
- Why does blowing over a spoonful of hot tea cools it? Does evaporation play a role? Does radiation play a role?
Solution:
Here, the convection plays the major role. The air coming from our mouth has less temperature than the hot tea. So, when we blow over the tea, the warm air rises up (due to less density) and the cool air goes down to the tea. In this way, the spoonful of hot tea cools.
Radiation takes place from a body when it has higher temperature than that of the surrounding. Since, the hot tea has higher temperature than the temperature of the surrounding, the heat transfer from the hot tea takes place to the surrounding through the radiation phenomena. - On a hot summer day we want to cool our room by opening the refrigerator door and closing all the windows and doors. Will the process work?
Solution:
No, the room will actually become warmer. When the door of a refrigerator is open in a closed room, the heat given out by the refrigerator to the room will be more than that taken from the room. Therefore, instead of decreasing, the temperature of the room will increase at a slower rate. - An ordinary electric fan does not cool the air, still it gives comfort in summer. Explain.
Solution:
An ordinary electric fan does not cool air. It circulates the air and the air which is more humid will be replaced by the less humid air. Air with less humidity is capable of holding more water vapor which thus allows the water in our body to evaporate easily. Due to this reason, though the fan does not cool the air, it gives comfort to our body. - Hot water pipes are painted black. Why?
Solution:
We should note that the good absorbers are also good emitters. Black color is a good absorber of heat and thus a good emitter. When hot water flows through a black painted pipe in a room, it radiates more heat than the pipe painted with other colors. Hence, hot water pipes are painted black. - Two blankets are warmer than the single blanket of double thickness. Explain.
Solution:
Air is a bad conductor of heat. Two blankets trap air between them. Due to the insulation provided by the air trapped between the two blankets, it feels warmer with two blankets than with a single blanket. - Ventilations are provided near the ceilings of the room. Why?
Solution:
Ventilations helps in circulation of air. The warm air has less density and thus rises up. It will then escape through the ventilations located near the ceiling. The cool air coming from the ventilations then rushes down into the room due to its less density. Hence, ventilations are provided near the ceilings of the room. - Finger sticks to the metal ice tray when taken from the refrigerators. Why?
Solution:
When we touch the metal ice tray, the heat tranformed from our finger melts the ice so that the film of water is formed between our finger and the tray. But, as soon as the water film is formed, it will again convert to ice because the metal ice tray is cold enough. - Stainless steel cooking pan are provided with the extra copper bottom. Why?
Solution:
Copper is a good conductor of heat. The conductivity of copper is larger than the conductivity of steel. Therefore when a cooking pan, fitted with extra copper sheet, is placed over a flame, more heat passes to the food. This helps in cooking the food fast. Hence, stainless steel cooking pan are provided with the extra copper bottom.
Numerical Problems
- A bar 0.20 m in length and cross-sectional area 2.5\(\times\) 10\(^{-4}\) sq. m. is ideally lagged. One end is maintained at 100\(^0\) C while the
other is maintained at 0\(^0\) C by immersion in melting ice. Calculate the rate at which the ice melts owing to the flow of heat along the bar. [Thermal conductivity of the material of the
bar =4\(\times\)10\(^2\)Wm\(^{-1}\)K\(^{-1}\)].
Solution:
length of a bar, l = 0.20 m
cross sectional area, A = 2.5\(\times\) 10\(^{-4}\) sq. m.
temperature of hot end, \(\theta_2\) = 100\(^0\) C
temperature of cold end, \(\theta_1\) = 0\(^0\) C
thermal conductivity of material of the bar, k = 4\(\times\)10\(^2\)Wm\(^{-1}\)K\(^{-1}\)
latent heat of fusion of ice, L = 3.36 \(\times\) 10\(^5\) J/kg
rate at which ice melts (say m) = ?
Now, if m is the mass of ice that melts in 1 sec. Then,
\[\frac{Q}{t}=mL\] Also, we have, \[\frac{Q}{t}=\frac{kA(\theta_2-\theta_1)}{l}\] Therefore, \[\begin{align*} mL&=\frac{kA(\theta_2-\theta_1)}{l}\\ m&=\frac{kA(\theta_2-\theta_1)}{Ll}\\ &=\frac{4\times 10^2 \times 2.5 \times 10^{-4} \times 100}{3.36 \times 10^5 \times 0.2}\\ \therefore m&=1.48 \times 10^{-4}\hspace{0.1cm} \text{kg/s} \end{align*} \] - Estimate the rate of heat loss through a glass window of area 2 m\(^2\) and thickness 3 mm when the
temperature of the room is 20\(^0\) C and that of air outside is 5\(^0\) C. [K for glass is 1.2 Wm\(^{-1}\) K\(^{-1}\)].
Solution:
area of window, A = 2 m\(^2\)
thickness , l = 3 mm = 3 \(\times\) 10\(^{-3}\) m
higher temperature, \(\theta_2\) = 20\(^0\) C
lower temperature, \(\theta_1\) = 5\(^0\) C
thermal conductivity of glass, k = 1.2 Wm\(^{-1}\) K\(^{-1}\)
rate of heat loss, \(\frac{Q}{t}\) = ?
Now,
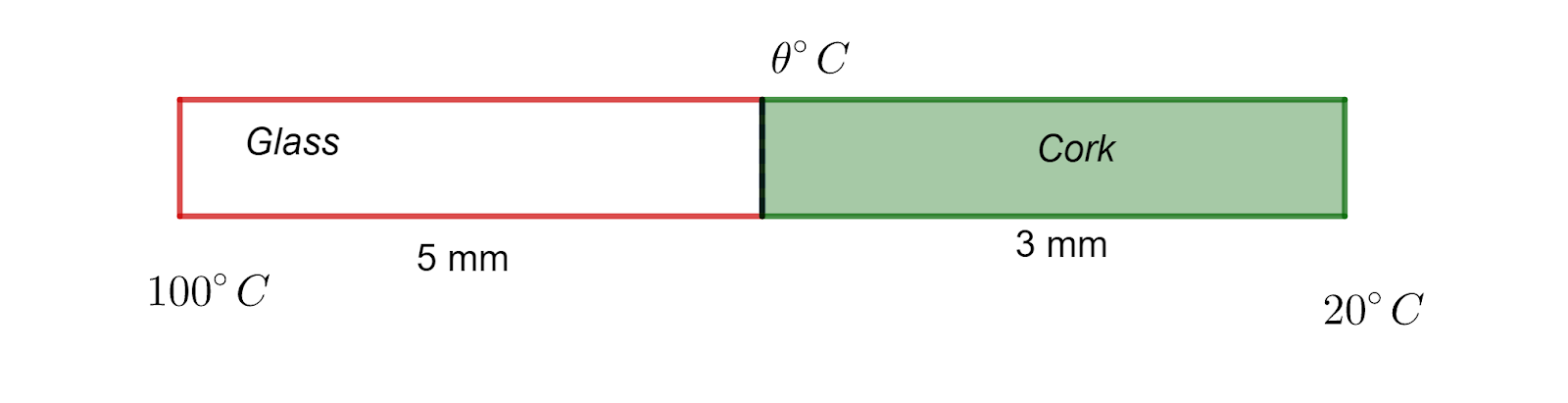
\[\begin{align*} \frac{Q}{t}&=\frac{kA(\theta_2-\theta_1)}{l}\\ &=\frac{1.2 \times 2 \times 15}{3\times 10^{-3}}\\ &=12000 \hspace{0.1cm} W \end{align*}\] Therefore, the rate of loss of heat through a glass window is 12 KW. - One face of a sheet of cork, 3 mm thick, is placed in contact with one face of a sheet of glass 5 mm thick, both sheets being 20 cm square.
The outer faces of this square composite sheet are maintained at 100\(^0\) C and 20\(^0\) C, the glass being at the higher mean temperature. Find the temperature
of the glass-cork interference. [ Given thermal conductivity of cork= 6.3\(\times\)10\(^{-2}\) Wm\(^{-1}\)K\(^{-1}\), thermal conductivity of glass=7.2\(\times\)10\(^{-1}\)Wm\(^{-1}\)K\(^{-1}\)].
Solution:
For cork-sheet,
thickness, l = 3 mm = 3 \(\times\) 10\(^{-3}\) m
area, A = 20 cm\(^2\) = 20 \(\times\) 10\(^{-4}\) m\(^2\)
temperature, \(\theta_1\) = 20 \(^\circ\) C
thermal conductivity, k = 6.3\(\times\)10\(^{-2}\) Wm\(^{-1}\)K\(^{-1}\)
Let \(\left(\frac{Q}{t}\right)_c\) be the rate of heat loss through cork sheet.
For glass-sheet,
thickness, l = 5 mm = 5 \(\times\) 10\(^{-3}\) m
area, A = 20 \(\times\) 10\(^{-4}\) m\(^2\)
temperature, \(\theta_2\) = 100 \(^\circ\) C
thermal conductivity, \textit{k} = thermal conductivity of glass=7.2\(\times\)10\(^{-1}\)Wm\(^{-1}\)K\(^{-1}\)
Let \(\left(\frac{Q}{t}\right)_g\) be the rate of heat loss through glass sheet.
Also, let \(\theta\) \(^\circ\) C be the temperature of the glass-cork interface.
Now,
\[\begin{align*} \left(\frac{Q}{t}\right)_c&=\frac{kA(\theta-20)}{l}\\ &=\frac{6.3 \times 10^{-2} \times 20\times 10^{-4}\times (\theta-20)}{3 \times 10^{-3}}\\ \end{align*}\] Also,
\[\begin{align*} \left(\frac{Q}{t}\right)_g&=\frac{kA(100-\theta)}{l}\\ &=\frac{7.2 \times 10^{-1} \times 20 \times 10^{-4}\times (100-\theta)}{5\times 10^{-3}}\\ \end{align*}\] At equilibrium state,
\[\begin{align*} \left(\frac{Q}{t}\right)_c&=\left(\frac{Q}{t}\right)_g\\ \frac{6.3 \times 10^{-2} \times 20\times 10^{-4}\times (\theta-20)}{3 \times 10^{-3}}&=\frac{7.2 \times 10^{-1} \times 20 \times 10^{-4}\times (100-\theta)}{5\times 10^{-3}}\\ 6.3 \times 10^{-2} \times (\theta-20)\times 5&=7.2 \times 10^{-1} \times (100-\theta) \times 3\\ 0.315(\theta-20)&=2.16(100-\theta)\\ 0.315 \theta - 6.3 &=216-2.16\theta\\ 2.475 \theta&=222.3\\ \theta&=89.8^\circ \hspace{0.1cm} C \end{align*}\] - Calculate the quantity of heat conducted through 2 sq.m. of a brick wall 2 cm thick in 1 hour if the temperature on one side is
5\(^0\) C and on the other side is 25\(^0\) C. (Thermal conductivity of brick=0.12 W/m/K).
Solution:
area, A = 2 \(m^2\)
thickness, l = 2 cm = 0.02 m
temperature difference, \(\theta_2-\theta_1\) = 25-5 = 20 \(^\circ\) C
thermal conductivity, k = 0.12 W/m/K
heat conducted in 1 hour = ?
Heat conducted per sec is given as, \[\begin{align*} \frac{Q}{t}&=\frac{kA(\theta_2-\theta_1)}{l}\\ &=\frac{0.12 \times 2 \times 20}{0.02}\\ &=240 \hspace{0.1cm} \text{W} \end{align*}\] Then, the heat conducted in 1 hour is,
\[=240\times 3600 = 864000 \hspace{0.1cm} \text{J}\] - The element of 1 KW electric fire has a surface area of 0.006m\(^2\). Estimate its working temperature. (The stefan constant=5.7\(\times\)10\(^{-8}\) Wm\(^{-2}\)K\(^{-4}\)).
Solution:
power, P = 1 KW = 1000 W
area, A = 0.006m\(^2\)
Stefan constant, \(\sigma\) = 5.7\(\times\)10\(^{-8}\) Wm\(^{-2}\)K\(^{-4}\)
temperature, \textit{T} = ?
From the Stefan's law,
\[\begin{align*} P&=\sigma A T^4\\ T^4&=\frac{P}{\sigma A}\\ &=\frac{1000}{5.7 \times 10^{-8} \times 0.006}\\ T&=\left[\frac{1000}{5.7 \times 10^{-8}\times 0.006}\right]^{\frac{1}{4}}\\ \therefore T&=1307.65 \hspace{0.1cm} \text{K} \end{align*}\] - The element of an electric fire with an output of 1.5 KW is a cylinder of 30 cm long and 0.2 cm in diameter. Calculate its temperature if it behaves as a black body. ( Follow the same procedure as above question. You need to use \(A=2\pi rl\) to find the area.)
- The sun is a black body of surface temperature about 6000 K. If the sun's radius is 7\(\times\)10\(^8\) m, calculate the energy per second radiated from its surface.
The earth is about 1.5\(\times\)10\(^{11}\) m from the sun. Assuming all the radiation from the sun falls on a sphere of this radius, estimate the energy per second per square meter received by the earth.
Solution:
temperature of sun, T = 6000 K
radius of sun, R = 7\(\times\)10\(^8\) m
distance of earth from sun, r = 1.5\(\times\)10\(^{11}\) m
energy received by earth per second per sq. metre, E = ?
From Stefan's law, the energy per second per sq. metre radiated from the sun's surface is,
\[\begin{align*} P&=\sigma A T^4\\ &=5.7 \times 10^8 \times 4\pi \times 7 \times 10^8 \times (6000)^4\\ &=4.54 \times 10^{26} \hspace{0.1cm} \text{Wm}^{-2} \end{align*}\] Energy per second per square metre received by the earth is,
\[\begin{align*} &=\frac{P}{4\pi r^2}\\ &=\frac{4.54 \times 10^{26}}{4\pi \times (1.5\times 10^{11})^2}\\ &=1605.69 \hspace{0.1cm} \text{Wm}^{-2} \end{align*}\] - The normal body temperature of a person is 97\(^0\) F. Calculate the rate at which heat is flowing out of his body through the clothes assuming the following values
Room temperature= 47\(^0\) F, surface of the body under clothes = 1.6 m\(^2\) conductivity of the cloth = 0.04 J/m-s-\(^0\) C, thickness of the cloth = 0.5 cm.
Solution:
\(\theta_1\) = 47 \(^\circ\) F = 8.33 \(^\circ\) C
\(\theta_2\) = 97 \(^\circ\) F = 36.11 \(^\circ\) C
temperature difference, \(\theta_2-\theta_1\) = 27.78 \(^\circ\) C
thickness of cloth, l = 0.5 cm = 0.005 m
area, A = 1.6 m\(^2\)
thermal conductivity, \textit{k} = 0.04 J/m-s-$^0$ C
rate of heat flow, \(\frac{Q}{t}\) = ?
Now, \[\begin{align*} \frac{Q}{t}&=\frac{kA(\theta_2-\theta_1)}{l}\\ &=\frac{0.04 \times 1.6 \times 27.78}{0.005}\\ &=355.58 \hspace{0.1cm} \text{W} \end{align*}\]


Comments
Post a Comment