Electrons | Complete notes with short answer questions and numerical problem solutions | Class 12 NEB Physics

Electrons

Introduction and background

Electron is the lightest subatomic particle. It carries a charge of -1.602176634 × 10^-19 C, which is considered the fundamental or basic unit of electric charge. The mass of an electron is 9.1093837015 × 10^-19 kg which is \(\frac{1}{1836}\) times the mass of a proton (a positively charged constituent of an atom).
Discovery of electrons:
The discharge tube experiment played an important role in the discovery of electrons. While studying the properties of cathode rays (1897 A.D.), J.J. Thomson (Nobel prize for Physics, 1906 ) found that the cathode rays are deflected in electric and magnetic fields which led scientists to believe that the cathode rays are made of tiny negatively charged particles. ( Note! In this chapter, we will learn how the electrons get affected by the electric and magnetic fields so you would know why scientists came in conclusion to identify the discovered particle as negatively charged electrons. ) These negatively charged particles are the electrons as we call them today. Thus the discovery of electrons is credited to J. J. Thomson.

Cathode ray tube used by J.J. Thomson. Image Source: Britannica

Millikan's oil drop experiment

Before taking the notes on this topic, lets have a brief insight on the topic to be more familiar with it. OK?

Robert Andrews Millikan Image source: Wikipedia
Robert A. Millikan, an American physicist devised a method to determine the charge of an electron. He performed a Oil drop experiment, which we know today as 'Millikan Oil-drop experiment' and was awarded the Nobel Prize for physics in 1923 for this classic experiment. The Millikan's setup for the oil drop experiment and the Millikan's oil drop experiment apparatus are shown in figures below.

Millikan's setup for the oil drop experiment Image source: Wikipedia

Millikan's oil drop experiment apparatus Image source: Wikipedia
Millikan and his coworkers repeated the experiment thousands of times and measured charges on so many drops to conclude that 1.6×10^-19 C as the charge of an electron.
Now with this brief insight, we are ready to take a dip into the topic for our notes.

Construction:

The basic design of the Miilikan oil drop experiment is shown in figure below. In his experiment, Millikan placed two accuratelt aligned parallel metal plates A and B separated by a distance of 1.5 cm with a small hole H of diameter 20 cm in the center of the upper plate A. The plates are enclosed in a chamber with glass walls. He used an atomiser to spray the tiny drops of oil above H. The chamber was illuminated by sending light horizontally through it. The drops can be seen by using a telescope perpendicular to the light beam. A drop then looks like a bright star. The electric field 'E' was applied by connecting a battery of several thousand volts across the plates A and B with A at higher potential and B at lower potential.
Some of the droplets acquire electric charge due to friction with air, but to give a drop an increased charge an X-ray tube was operated near the chamber to ionise the air such that the electrons then attaches to the oil drops. The motion of the drop was measured by means of a scale in the eyepiece of the telescope.

Theory:

Millikan first measured the terminal velocity of the oil drop through the air without applying the electric field. He then charged the oil-drop and applied an electric field to oppose gravity. The drop now moved with a different terminal velocity which was again measured.

(i) Motion of oil drop under the effect of gravity alone:

Suppose r be the radius of an oil drop, ρ be its density and η be the viscosity of air. When the drop in absence of electric field, falls steadily under gravity with terminal velocity v₁ , \[F_v+U=W\] where, F_v is the viscous force on the oil drop, U is the upthrust due to air and W is the weight of the oil drop.
From Stoke's law, \[F_v=6 \pi \eta r v_1\] If σ is the density of air then, \[U=\frac{4}{3} \pi r^3 \sigma g\] Now, \[\begin{align*} F_v+U&=W\\ 6\pi \eta r v_1 + \frac{4}{3} \pi r^3 \sigma g &= \frac{4}{3} \pi r^3 \rho g\\ 6\pi \eta r v_1& = \frac{4}{3} \pi r^3 g (\rho-\sigma)\\ \therefore r&=\sqrt{\frac{9 \eta v_1}{2(\rho-\sigma)g)}}\hspace{0.1cm} \text{ ... (i)}\\ \end{align*}\] From this relation, radius of an oil drop can be obtained.

(ii) Motion of oil drop in presence of electric field:

Suppose the drop now gains a charge q and an electric field of intensity E is applied to oppose the gravity. The terminal velocity of drop now becomes smaller i.e., v₂ .
The electrostatic force on the drop due to E is then, \[F_e=qE\] Viscous force is, \[F_v=6 \pi \eta r v_2\] Then, \[\begin{align*} F_e+U&=F_v+W\\ F_e&=(W-U)+F_v\\ qE&=\frac{4}{3} \pi r^3 (\rho-\sigma)g + 6 \pi \eta r v_2\\ qE&=6 \pi \eta r v_1 + 6\pi \eta r v_2\\ q&=\frac{6 \pi \eta r (v_1+v_2)}{E}\\ \therefore q&=\frac{6 \pi \eta(v_1+v_2)}{E}\sqrt{\frac{9 \eta v_1}{2(\rho-\sigma)g}}\hspace{0.1cm} \text{(from (i))}\\ \end{align*}\] Alert! In the third step, I have used the relation of (W-U) from the first subtopic i.e., F_v+U=W .
From this relation, the value of charge on the oil drop can be obtained. Millikan and his coworkers found that each drop had a charge that was a small integral multiple of a basic value e = 1.6×10^-19 C. From this observation, Millikan concluded that e = 1.6×10^-19 C is the charge on an electron. If one electron is attached to a drop, the charge on the drop is e. If n electrons are attached to a drop, the charge on the drop is ne, wwith n as an integer. This is also called the Quantization of charge .

Q.1 Describe Millikan's oil drop experiment and explain how it suggests quantization of charge. ( See the solution above. )

Motion of electrons in electric field

Suppose a horizontal beam of electrons moving with a velocity v enters midway bwteen the two parallel plats as shown in figure. Upper plate is at higher potential and lower is at lower potential. If V be the potential difference between the plates d distance apart, then the electric field intensity is, \[E=\frac{V}{d}\] Hence the force on an electron is, \[F=eE=e\frac{V}{d}\] which is directed towards the positive plate.
Since, the electric field intensity is vertical, the horizontal motion of electron is unaltered as no horizontal force acts on it on entering the plates. Thus, the horizontal velocity, v of an electron remains unaffected. This is similar to the motion of a projectile projected horizontally under gravity. The vertical acceleration due to gravity does not affect the horizontal motion.
If m be the mass of electron, the force acting on an electron is, \[F=ma\] So, the vertical acceleration is, \[\begin{align*} a&=\frac{F}{m}\\ &=\frac{eE}{m}\\ &=\frac{eV}{md}\text{ ... (i)}\\ \end{align*}\] Let, the electron reaches at point P(x,y) at a time t , then,
For horizontal motion,
\[\begin{align*} x&=u_x t +\frac{1}{2} a_x t^2\\ &=vt\\ t&=\frac{x}{v}\hspace{0.1cm} \text{ ... (ii)}\\ \end{align*}\]
For vertical motion,
\[\begin{align*} y&=u_yt+\frac{1}{2}a_y t^2\\ &=\frac{1}{2} at^2\\ &=\frac{1}{2} \times \frac{eV}{md} t^2 \hspace{0.1cm} \text{(from (i))}\\ &=\frac{1}{2} \frac{eV}{md}\left(\frac{x}{v}\right)^2 \hspace{0.1cm} \text{(from (ii))}\\ \therefore y&=\left(\frac{eV}{2mdv^2}\right)x^2 \hspace{0.1cm} \text{ ... (iii)}\\ \end{align*}\] Comparing equation (iii), with the equation of parabola \[y=Ax^2+bx+c\] we find that equation (iii) is an parabolic equation with \[A=\frac{eV}{2mdv^2}\] \[B=0\] \[C=0\] Hence, the motion of electron beam in an electric field is parabolic in nature.

Q.2 Show that the motion of an electron in an electric field is parabolic in nature. ( See the solution above. )

Motion of electron beam in a unifom magnetic field

Consider an electron beam, moving with a speed v, which enters a uniform magnetic field of magnitude B acting perpendicular to the direction of motion of an electron beam as in figure.
The force acting on an electron is, \[\begin{align*} F&=Bevsin\theta\\ &=Bev \hspace{0.1cm} \because \theta=90^\circ\\ \end{align*}\] The magnetic force deflects the electrons without altering its speed. It is always normal to the path of the beam. In uniform field, the magnetic force is constant in magnitude and the beam travels in a circle of radius r. Here, the centripetal force is provided by the magnetic force. So, \[\begin{align*} F_m&=F_c\\ Bev&=\frac{mv^2}{r}\\ \therefore r&=\frac{mv}{Be} \hspace{0.1cm} \text{ ... (i)}\\ \end{align*}\] r is the radius of circular path of an electron.
From (i), \[\begin{align*} r&=\frac{mv}{Be}\\ v&=\frac{Ber}{m}\\ r\omega&=\frac{Ber}{m}\\ \omega&=\frac{Be}{m}\\ 2 \pi f&=\frac{Be}{m}\\ \therefore f&=\frac{Be}{2 \pi m}\\ \end{align*}\] This result shows that f is independent of the radius of circular path and velocity of the electron beam.

Q.3 Show that electron motion in magnetic field is circular. Prove that frequency and time period are independent with the velocity of electron. ( See the solution above. For time period, use the relation \(T=\frac{1}{f}\) in above expression. )

Thomson's experiment to determine specific charge of electrons

Let's have some understanding of basic terms before writing the notes on this topic. OK? The specific charge of an electron is defined as the ratio of charge of an electron per unit mass of an electron. The basic physics behind his famous experiment to measure the specific charge of an electron is described in the section below. Thomson measured the specific charge of an electron by measuring how much the cathode rays are deflected by the electric and magnetic fields.
Now lets write note! Ok?
Construction:

Figure shows the basic design of Thomson's experiment to measure specific charge of an electron \(\frac{e}{m}\). A large potential difference V is applied between the cathode C and anode A such that a narrow beam of electrons, ejected from the cathode, passes through the holes in the anode A. The beam passes through the region between the two metal plates P₁ and P₂ separated by distance d and then strikes the end of the tube. Plate P₁ is connected to the positive terminal of a power supply and P₂ to the negative. Thus a constant potential difference is maintained between them. E is the electric field in the region between the plates which is directed downward direction in figure and exerts a force in the upward direction on the electrons (towards S₂).
A magnetic field B can also be applied in the region between the plates by passing electric currents in circular coils (represented by dashed circle in figure). This field is perpendicular to the electric field as well as to the undeviated path of the cathode rays. If magnetic field alone is present, the electrons moves in a circular arc and deviates in a downward direction (towards S₁) in the figure).
Theory:
If both the electric fields and the magnetic fields are switched on and the values are chosen such that, \[\begin{align*} F_m&=F_e\\ Bev&=eE\\ \therefore v&=\frac{E}{B}\hspace{0.1cm} \text{ ... (i)}\\ \end{align*}\] In this case, the electron beam will pass undeflected and pass towards S in the figure.
If V be the potential difference between the anode A and the cathode C, the speed of the electrons coming out of A is, \[\begin{align*} eV&=\frac{1}{2} mv^2\\ eV&=\frac{1}{2} m \left(\frac{E}{B}\right)^2 \hspace{0.1cm} \text{(from (i))}\\ \frac{e}{m}&=\frac{E^2}{2B^2 V}\\ \end{align*}\] This relation gives the value of specific charge of an electron.

Q.4 Describe J.J. Thomson's experiment with necessary theory behind the determination of specific charge of electron. ( See the solution above.)

Q.5 Beams of electrons and protons having the same initial K.E. enter normally into an electric field, which beam will be more curved? Justify.
Solution:
When this charged particles enters an electric field, the electric field exerts force upon them which makes their path curved. So, here the centripetal force is provided by the force due to an electric field. If q be the charge, m be it's mass and v be its velocity then, \[\begin{align*} qE&=\frac{mv^2}{r}\\ qE&=2 \times \frac{1}{2} \frac{mv^2}{r}\\ &=2 \times \text{K.E.}\frac{1}{r}\\ \therefore r&=\frac{2 \times \text{K.E.}}{qE}\\ \end{align*}\] Since, the radius of curved path r does not depend on mass, and the magnitude of charge i.e., q, electric field acting on them E and K.E. are same, we conclude that the both charge will be curved by same amount.
Q.6 The value of e/m is constant for cathode rays, but not for positive rays. Explain.
Solution:
The charge of electron e and its mass m are constant. So the value of \(\frac{e}{m}\) is constant. However, the mass of positive ions for different gases is different, due to which their specific charge is not constant.
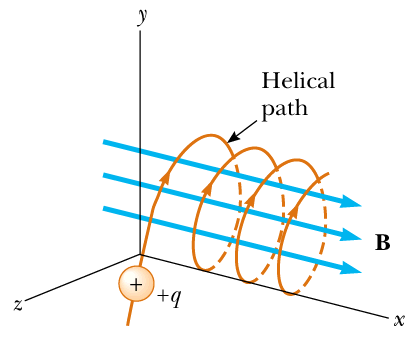
Q.7 A charged particle is fired into a cubical region of space where there is uniform magnetic field. Outside the region, there is no magnetic field. Is it possible that the particle will remain inside the cubical region? Explain.
Solution:
When the charged particle enters the magnetic field, it experiences the Lorentz force \[\vec{F}=qvBsin\theta\] where θ is the angle between the velocity of charged particle and direction of the magnetic field.
If θ=0⁰ or 180⁰, the path of charged particle will be a straight line since no force act on it. However, if θ=90⁰, the path of charged particle will be circular. For other angles, it's path will be helical (shown in figure).

Image credit: Physics Exams Thus, we can conclude that, if the path of a charged particle is straight line (cases discussed above), it emerges out of the cubical region. For circular path (as discussed above), if the diameter of the circle is less than the edge of the cube, the particle will remain inside the cubical region. For other angles, since the particle is in helical motion (linear+circular), the particle will leave the cubical region even if the diameter of circle is less than the edge of cube.
Q.8 An electron and a proton move with the same speed in a uniform magnetic field of equal magnitude. Compare the radii of their circular path.
Solution:
When the charged particle enters the uniform magnetic field, it moves on a circular path. The necessary centreipetal force is provided by the force due to magnetic field. So, \[\begin{align*} Bqvsin\theta&=\frac{mv^2}{r}\\ Bqsin\theta&=\frac{mv}{r}\\ \therefore r&=\frac{mv}{Bqsin\theta}\\ \end{align*}\] Since, B, v, q and θ is same for both electron and proton in our case, we can thus write, \[r\propto m\] As the mass of proton is 1836 times that of a mass of electron. \[m_p=1836m_e\] \[r_p=1836r_e\] Hence, the radii of circular path for proton is greater than that of an electron.
Q.9 What property of cathode rays indicates that they consist of electrons?
Solution:
When charged particle enters the magnetic field or electric field, it deflects. The nature of deflection of positive and negative charges are different. Furthermore, the specific charge of cathode rays and electron is same. This two reasons concluded that cathode rays consist of electrons.
Q.10 Compare the specific charge of an electron to that of a proton.
Solution:
Hints: Specific charge of a charged particle is defined as the ratio of charge and mass of that particle. Try it! Q.11 Cathode rays cannot be regarded as electromagnetic waves. Why?
Solution:
Hints: Electromagnetic waves are not deflected by electric or magnetic fields.
Q.12 The terminal velocity of the drop will be changed in the Millikan's oil drop experiment if more intense X ray is passed. Why?
Solution:
In Millikans oil drop experiment, X ray is used to ionise the air. As intense X ray is passed, more air will be ionised such that more electrons will be attached to the oil drop. As the charge on oil drop increases, its velocity will also be changed.

Q.13 An electron having 500 eV energy enters at right angle to a uniform magnetic field of 10^-4 T. If its specific charge is 1.75× 10¹¹ C/kg. Calculate the radius of its circular orbit.
Solution:
Given,
K.E. of electron = 500 eV = 500×1.6×10^-19 J = 8×10^-17 J
magnetic field strength, B = 10^-4 T
specific charge, \(\frac{e}{m}\) = 1.75× 10¹¹ C/kg
potential difference, \(V\) = 500 V (\(\because\) eV=500 electron Volt)
radius of circular path, r = ?
When an electron enters the uniform magnetic field, it follows a circular arc. The necessary centripetal force is provided by the magnetic force. \[\begin{align*} Bev&=\frac{mv^2}{r}\\ r&=\frac{mv}{Be}\\ \end{align*}\] The kinetic energy of an electron is equal to the work done on it. So, \[\begin{align*} \text{K.E.}&=eV\\ \frac{1}{2} m v^2&=e \times 500\\ v^2&=1000 \times \frac{e}{m}\\ &=1000 \times 1.75 \times 10^{11}\\ &=1.75\times 10^14\\ \therefore v&=1.32 \times 10^7 \hspace{0.1cm}m/s\\ \end{align*}\] Substituting this in relation of r, we get, \[\begin{align*} r&=1.75 \times 10^{14} \times \frac{1}{B\frac{e}{m}}\\ &=\frac{1.32 \times 10^{7}}{10^{-4}\times 1.75 \times 10^{11}}\\ \therefore r&=0.75 \hspace{0.1cm} m\\ \end{align*}\] Hence, the required radius of circular orbit is 0.75 m.
Q.14 In a Millikan's oil drop experiment, a drop is observed to fall with a terminal speed 1.4 mm/s in the absence of electric field. When a vertical electric field of 4.9×10⁵ V/m is applied, the droplet is observed to continue to move downward at a lower terminal speed 1.21 mm/s. Calculate the charge on the drop. (Density of oil = 750 kg/m³, viscosity of air = 1.81×10^-5 kg/ms, density of air = 1.29 kg/m³).
Solution:
Given,
density of oil, ρ = 750 kg/m³
density of air, σ = 1.29 kg/m³
viscosity of air, η = 1.81×10^-5 kg/ms
In absence of electric field,
terminal velocity, v₁ = 1.4 mm/s = 1.4×10^-3 m/s
In presence of electric field,
electric field strength, E = 4.9×10⁵ V/m
terminal speed, v₂ = 1.21 mm/s = 1.21×10^-3 m/s
Now,
\[\begin{align*} q&=\frac{6 \pi \eta (v_1-v_2)}{E} \times \sqrt{\frac{9\eta v_1}{2(\rho-\sigma)g}}\\ &=\frac{6 \pi \times 1.81\times 10^{-5}\times (1.4 \times 10^{-3} - 1.21 \times 10^{-3})}{4.9 \times 10^5} \times \sqrt{\frac{9 \times 1.81 \times 10^{-5} \times 1.4 \times 10^{-3}}{2 (750-1.29)\times 9.8}}\\ \therefore q&=5.21\times 10^{-19}\hspace{0.1cm} C \\ \end{align*}\] Hence, the charge on oil drop is 5.21×10^-19 C.
Alert! Have you noticed one thing here? The general formula of q is ,\[q=\frac{6 \pi \eta (v_1+v_2)}{E} \times \sqrt{\frac{9\eta v_1}{2(\rho-\sigma)g}}\] but I have replaced + with - sign in between v₁ and v₂. It is because though the electric field is applied, the oil drop continues to move in downward direction and the formula here is for drop moving in the upward direction. For more detail, you can see the derivation of q above (Theory of Millikan's Oil drop experiment) and reverse the direction of v₂. Ok? If you still have doubt, please comment in the comment section.
Q.15 A beam of electrons, moving with velocity of 10⁷ m/s, enters midway between two horizontal plates in the direction parallel to the plates which are 5 cm long and 2 cm apart and have a p.d. of V volts between them. Calculate V if the beam is deflectedd so that it just grazes the edge of the plate. (Assume e/m = 1.76×10¹¹ C/kg).
Solution:
Given,
velocity of electron beam, v = 10⁷ m/s
length of plates, D = 5 cm = 0.05 m
distance between plates, d = 2 cm = 0.02 m
e/m = 1.76×10¹¹ C/kg
potential difference, V = ?
Now,
When the beam just grazes the plate, it travels distance D along the horizontal inside the plates. Thus, \[x=D\] Also, since the electron beam enters midway between the plates, as it grazes, it travels the vertical distance of d/2 i.e., \[y=d/2=0.01 \hspace{0.1cm} m\] Then, \[\begin{align*} y&= \frac{eV}{2mdv^2}D^2\\ 0.01&=\frac{1.76 \times 10^{11} \times V}{2 \times 0.02 \times 10^{14}}\times (0.05)^2\\ V&=\frac{0.01\times 2\times \times 0.02 \times 10^{14}}{1.76 \times 10^{11}\times 0.05^2}\\ \therefore V&=90.90 \hspace{0.1cm} V\\ \end{align*}\] Hence, the potential difference between the plates is 90.90 V.
Q.16 Calculate the radius of a water drop which would just remain suspended in an electric field of 300 V/cm and charged with one electron.
Solution:
Given,
electric field, E = 300 V/cm = 300×100 V/m = 3×10⁴
charge, q = e = 1.6×10^-19 C
radius of water drop, r = ?
For the water drop to remain stationary, the weight of the water drop must be balanced by the force on it due to electric field.
\[\begin{align*} qE&=mg\\ eE&=\frac{4}{3}\pi r^3 \rho g\\ r^3&=\frac{1.6\times 10^{-19}\times 3\times 10^4\times 3}{4 \pi\times 1000\times 9.8}\\ \therefore r&=4.89\times 10^{-7} \hspace{0.1cm} m\\ \end{align*}\] Hence the radius of water drop is 4.89×10^-7 m .
Q.17 An electron beam after being accelerated from rest through a potential difference of 5 KV in vacuum is allowed to impinge normally on a fixed surface. If the incident current is 50μ A. Determine the force exerted on the surface assuming that it brings the electrons to rest. Take mass of electron is 9.1×10^-31 Kg.
Solution:
Given,
potential difference, V = 5 kV = 5×10³ V
current, I = 50 μ A = 50 ×10^-6 A
force exterted on electron, F = ?
mass of electron, m = 9.1×10^-31 Kg
Now,
The work done on electron when it is accelerated through p.d. of 5×10⁴ V is equal to its kinetic energy.
\[\begin{align*} \frac{1}{2} m v^2&=eV\\ v&=\sqrt{\frac{2eV}{m}}\\ \end{align*}\] If n be the number of electrons striking the surface then,
\[\begin{align*} I&=\frac{q}{t}\\ &=\frac{ne}{t}\\ \end{align*}\] We know, Force exerted on the surface = change in momentum / time of impact Now,
\[\begin{align*} F&=\frac{nmv}{t}\\ &= \frac{I}{e}\times m \times \sqrt{\frac{2eV}{m}}\\ &=\frac{50 \times 10^{-6}}{1.6 \times 10^{-19}} \times 9.1\times 10^{-31} \times \sqrt{\frac{2 \times 1.6 \times 10^{-19} \times 5 \times 10^3}{9.1\times 10^{-31}}}\\ \therefore F&=1.19 \times 10^{-8} \hspace{0.1cm} N \\ \end{align*}\] Hence, the force exerted on the surface is 1.19×10^-8 N.
Q.18 In a Millikan apparatus the horizontal plates are 1.5 cm apart. With the electric field switched off an oil drop is observed to fall with the steady velocity 2.5×10^-2 cm/s. When the field is switched on the upper plate being positive, the drop just remains stationary when the p.d. between the plates is 1500 V. Calculate the radius of the drop and the number of electronic charges neglecting air density. (Given, density of oil = 900 kg/m³ and viscosity of air = 1.8×10^-5 Nsm^-2).
Solution:
Given,
distance between plates, d = 1.5 cm = 0.015 m
In absence of electric field,
terminal velocity, v₁ = 2.5×10^-2 cm/s = 2.5×10^-4 m/s
In presence of electric field, the drop remains stationary ( thus no terminal velocity .
p.d. between the plates, V = 1500 V
density of oil, ρ = 900 kg/m³
viscosity of air, η = 1.8×10^-5 Nsm^-2
radius of drop, r = ?
We should note one thing here! Since the density of air is neglected, we donot take into account the 'upthrust'.
When the electric field is switched off,
weight of an oil drop = viscous force \[\begin{align*} mg&=6 \pi \eta r v\\ \frac{4}{3} \pi r^3 \rho g&=6\pi \eta r v\\ r&=\sqrt{\frac{9 \eta v}{2 \rho g}}\\ &=\sqrt{\frac{9 \times 1.8 \times 10^{-5}\times 2.5 \times 10^{-4}}{2\times 900 \times 10}}\\ \therefore r&= 1.5 \times 10^{-6} \hspace{0.1cm} m\\ \end{align*}\] Now, when the electric field is switched off and the drop remains stationary.
force on drop due to electric field = weight of drop \[\begin{align*} qE&=mg\\ q&=\frac{mg}{E}\\ &=\frac{4}{3} \pi r^3 \rho g \times \frac{d}{V} \hspace{0.1cm} \because E=\frac{V}{d}\\ &=\frac{4}{3}\times \pi \times (1.5 \times 10^{-6})^3 \times 900 \times 10 \times \frac{0.015}{1500}\\ ne&=12.72 \times 10^{-19}\\ n&=\frac{12.72 \times 10^{-19}}{1.6 \times 10^{-19}}\\ \therefore n&=8\\ \end{align*}\]
Q.19 In a Thomson experiment voltage across the plates is 50 V and the distance between them is 3 cm. The magnetic field applied to make the beam undeflected is 10^-4 T. What is the velocity of the electron passing between the plates?
Solution:
Given,
p.d. across the plates, V = 50 V
distance between plates, d = 3 cm = 0.03 m
magnetic field strength, B = 10^-4 T
velocity of electron, v = ?
Now,
For the undeflected beam,
force due to magnetic field = force due to electric field Now,
\[\begin{align*} Bev&=eE\\ v&=\frac{E}{B}\\ &=\frac{V}{dB}\\ &=\frac{50}{0.03\times 10^{-4}}\\ \therefore v&=1.67 \times 10^7 \hspace{0.1cm} m/s\\ \end{align*}\] Hence, the velocity of electron is 1.67×10⁷ m/s .
Q.20 An oil drop of mass 3.25×10^-15 kg falls vertically with uniform velocity, through the air between vertical parallel plates which are 2 cm apart. When a p.d. of 1000 V is applied to the plates, the drop moves to the positively charged plate being inclined at 45⁰ to the vertical. Calculate the charge on the drop.
Solution:
Given,
mass of oil drop, m = 3.25×10^-15 kg
distance between the plates, d = 2 cm = 0.02 m
p.d., V = 1000 V
inclination to the vertical, θ = 45⁰
charge on the drop, q = ?
Let v₁ and v₂ be the velocity components of the oil drop as shown in figure such that, \[v_1=vcos45^\circ\] and, \[v_2=vsin45^\circ\]

We can see from the figure,
\[mg=6\pi \eta r v_1\] and, \[qE=6 \pi \eta r v_2\] Dividing this two equations, we get, \[\begin{align*} \frac{qE}{mg}&=\frac{vsin45^\circ}{vcos45^\circ}\\ \frac{qE}{mg}&=1\\ q&=\frac{mg}{E}\\ &=\frac{mgd}{V}\\ \therefore q&=6.37 \times 10^{-19} \hspace{0.1cm} C\\ \end{align*}\] Hence, the charge on the drop is 6.37×10^-19 C .