Magnetic field | Class 12 NEB Physics | Numerical Problems Discussion

Two galvanometers, which are otherwise identical, are fitted with different coils. One has a coil of 50 turns and resistance 10 Ω while the other has 500 turns and a resistance of 600 Ω. What is the ratio of the deflection when each is connected in turns to a cell of emf 25 V and internal resistance 50 Ω?
Solution:
For galvanometer coil 1,
number of turns, N₁ = 50
resistance, R₁ = 10 Ω

For galvanometer coil 2,
number of turns, N₂ = 50
resistance, R₂ = 10 Ω

emf of a cell, E = 25 V
internal resistance of a cell, r = 50 Ω

Let \(\alpha_1\) and \(\alpha_2\) be the deflection of the galvanometer coil 1 and 2 respectively.
\(\frac{\alpha_1}{\alpha_2}\) = ?

We know, the restoring torque on a coil is equal to the deflecting torque. \[\begin{align*} \tau &= BINA\\ k \alpha & = BINA\\ \end{align*}\] where k is the restoring torque per unit twist of the suspension wire.
So, \[I_1 = \frac{k \alpha_1}{B N_1 A} \hspace{0.1cm} ... \hspace{0.1cm} (i)\]
\[I_2 = \frac{k \alpha_2}{B N_2 A} \hspace{0.1cm} ... \hspace{0.1cm} (ii)\] I₁ and I₂ are the current flowing through the coil 1 and 2 respectively.
Also, \[I_1 = \frac{E}{R_1 + r} \hspace{0.1cm} ... \hspace{0.1cm} (iii)\]
\[I_2 = \frac{E}{R_2 + r} \hspace{0.1cm} ... \hspace{0.1cm} (iv)\]
From (i) and (iii), we get,
\[\frac{k\alpha_1}{B N_1 A } = \frac{E}{R_1 + r} \hspace{0.1cm} ... \hspace{0.1cm} (v)\]
From (ii) and (iv), we get,
\[\frac{k\alpha_2}{B N_2 A } = \frac{E}{R_2 + r} \hspace{0.1cm} ... \hspace{0.1cm} (vi)\]
Dividing equation (v) by (vi), we get,
\[\begin{align*} \frac{\alpha_1 N_2}{N_1 \alpha_2}&=\frac{R_2 + r}{R_1 + r}\\ \frac{\alpha_1 \times 500}{50 \times \alpha_2}&=\frac{650}{60}\\ \frac{\alpha_1}{\alpha_2}&=\frac{13}{12}\\ \end{align*}\]
Conclusion: The required ratio of deflection is \(\frac{13}{12}\).

A siver wire has 1×10³⁰ free electrons per cubic meter, a cross sectional area of 2 mm² and carries a current of 5 A. Calculate the force acting on each electron if the wire is now placed in a magnetic field of flux density 0.15 T which is perpendicular to the wire.
Solution:
free electron density, n = 1×10³⁰/m³
cross - sectional area, A = 2 mm² = 2×10^-6 m²
current, I = 5 A
magnetic flux density, B = 0.15 T
force acting on each electron, F_e = ?

We know, \[F_e = B e v_d\] where, \(v_d\) is the drift velocity of electron.
Also, \[\begin{align*} I & = neA v_d\\ v_d & = \frac{I}{neA}\\ &= \frac{5}{10^{30}\times 1.6 \times 10^{-19} \times 2 \times 10^{-6}}\\ \therefore v_d & = 1.5 \times 10^{-5} \hspace{0.1cm} m/s\\ \end{align*}\] Then, \[\begin{align*} F_e & = Bev_d\\ & = 0.15 \times 1.6 \times 10^{-19} \times 1.5 \times 10^{-5}\\ \therefore F_e & = 3.6 \times 10^{-25} \hspace{0.1cm} N \\ \end{align*}\]
Conclusion: The force acting on each electron is 3.6×10^-25 N.

A horizontal straight wire 5 cm long weighing 1.2 g/m is placed perpendicular to a uniform horizontal magnetic field of flux density of 0.6 T. If the resistance per unit length of the wire is 3.8Ω/m, calculate the p.d. that has to be applied between the ends of the wire to make it self-supporting.
Solution:
mass per unit length of wire, \(\frac{m}{l}\) = 1.2 g/m = 1.2×10^-3 kg/m
length, l = 5 cm = 0.05 m
magnetic flux density , B = 0.6 T
resistance per unit length, \(\frac{R}{l}\) = 3.8 Ω/m
So, \[R = 3.8 \times l = 3.8 \times 0.05 = 0.19 \hspace{0.1cm}\Omega\] potential difference, V = ?

For the wire to be self-supporting, force due to magnetic field on it (in the upward direction given by Fleming's left hand rule) is equal to the downward force of gravity. \[\begin{align*} F_m&=F_g\\ BIl&=mg\\ I&=\frac{m}{l} \times \frac{g}{B}\\ &= 1.2 \times 10^{-3} \times \frac{10}{0.6}\\ \therefore I & = 0.02 \hspace{0.1cm} A \\ \end{align*}\]
Then, \[\begin{align*} V&=I \times R\\ &= 0.02 \times 0.19 \\ & = 3.8 \times 10^{-3} \hspace{0.1cm} V\\ \end{align*}\]
Conclusion: The required potential difference is 3.8×10^-3V.

A coil consisting of 100 circular loops with radius 60 cm carries a current of 5 A. Find the magnetic field at a point along the axis of the coil, 80 cm from the centre. (μ₀) = 4π×10^-7 T/mA)
Solution:
number of turns, n = 100
radius of circular loop / coil, a = 60 cm = 0.60 m
current, I = 5 A
magnetic field at x = 0.80 m, B = ?
μ₀ = 4π×10^-7 T/mA

Now, \[\begin{align*} B&=\frac{\mu_0 n I a^2}{2 (a^2 + x^2)^{3/2}}\\ &=\frac{ 4 \pi \times 10^{-7} \times 100 \times 5 \times 0.60^2}{2(0.60^2 + 0.80^2)^{3/2}}\\ \therefore B&= 1.13 \times 10^{-4} \hspace{0.1cm} T\\ \end{align*}\]
Conclusion: The required magnetic field is 1.13×10^-4 T.

A straight conductor of length 5 cm carries current of 1.5 A. The conductor experiences a magnetic force of 4.5×10^-3N when it is placed in a magnetic field of 0.9 T. What angle the conductor makes with magnetic field?
Solution:
length, l = 5 cm = 0.05 m
current, I = 1.5 A
force due to magnetic field, F = 4.5×10^-3 N
magnetic field, B = ?

Now, \[\begin{align*} F&=BIlsin\theta\\ 4.5 \times 10^{-3}&=0.9 \times 1.5 \times 0.05 \times sin\theta\\ sin\theta&=\frac{4.5 \times 10^{-3}}{0.9 \times 1.5 \times 0.05}\\ \theta&=sin^{-1}(\frac{1}{15})\\ \therefore \theta&=3.8^\circ\\ \end{align*}\]
Conclusion: The required angle is 3.8⁰.

A horizontal wire, of length 5 cm and carrying a current of 2 A, is placed in the middle of a long solenoid at right angles to its axis. The solenoid has 1000 turns per meter and carries a steady current I. Calculate I if the force on the wire is equal to 10^-4 N. (μ₀ = 4π10^-7 H/m).
Solution:
length of wire, l = 5 cm = 0.05 m
current, I = 5 A
number of turns per unit length of solenoid, n = 1000
force on the wire, F = 10^-4 N
μ₀ = 4π10^-7 H/m
Remember that the magnetic field of the solenoid is along the axis of the solenoid. So, when the wire is placed perpendicular to the solenoid, it experiences the force due to this magnetic field of solenoid.
The force experienced by the wire is, \[\begin{align*} F&=BIl\\ 10^{-4}&=B \times 2 \times 0.05 \\ B&=10^{-3} \hspace{0.1cm} T \\ \end{align*}\] Also, \[\begin{align*} 10^{-3}&=4 \pi \times 10^{-7} \times 1000 \times I \\ \therefore I& = 0.8 \hspace{0.1cm} A\\ \end{align*}\]
Conclusion: The required current through the wire is 0.8 A.

The coil of a moving coil galvanometer has 50 turns and its resistance is 10 Ω. It is replaced by a coil having 100 turns and resistance 50 Ω . Find the factor by which the current and voltage sensitivities change. Solution:
For galvanometer coil 1,
number of turns, N₁ = 50
resistance, R₁ = 10Ω
When the coil is replaced, let the new coil be a coil 2.
For galvanometer coil 2,
number of turns, N₂ = 100
resistance, R₂ = 50Ω

Let C₁ and C₂ be the current sensitivity of coil 1 and coil 2 respectively. Similarly, V₁ and V₂ be their voltage sensitivity.
Now, \[C_1=\frac{BN_1 A}{k}\] \[C_2=\frac{BN_2 A}{k}\] where k is the restoring torque per unit twist of the suspension wire.

Dividing this two equations, \[\begin{align*} \frac{C_2}{C_1}&=\frac{N_2}{N_1}\\ &=\frac{100}{50}\\ \therefore \frac{C_2}{C_1} = 2\\ \end{align*}\]
Also, \[V_1=\frac{BN_1 A}{kR_1}\] \[V_2=\frac{BN_2 A}{kR_2}\]
Dividing this two equations, we get, \[\begin{align*} \frac{V_2}{V_1}&=\frac{N_2 R_1}{N_1 R_2}\\ \therefore \frac{V_2}{V_1}&=\frac{2}{5}\\ \end{align*}\]
Conclusion: Thus, the factor by which current sensitivities and voltage sensitivities change are 2 and 2/5 respectively.

A 60 cm long wire of mass 10 g is suspended horizontally in a transverse magnetic field of flux density 0.4 T through two springs at its two ends. Calculate the current required to pass through the wire so that there is zero tension in the springs.
Solution:
Hints!
length, l = 60 cm = 0.60 m
mass of wire, m = 10 g = 10× 10^-3 kg
magnetic flux density, B = 0.4 T
current, I = ? (for zero tension in the springs)

For zero tension in the string, the magnetic force on the wire should be balanced by the force of gravity. So just use the relation \[F_m = F_g\] where, \[F_m = BIl\]

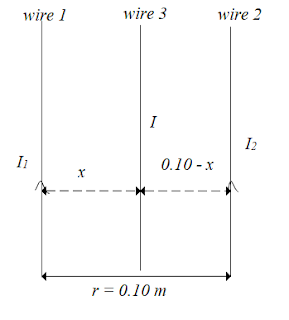
Two long parallel conductors carry respectively currents of 12 A and 8 A in the same direction. If the wires are 10 cm apart, find where a third parallel wire also carrying a current must be placed so that the force experienced by it will be zero.
Solution:

Current on wire 1, I₁ = 12 A
Current on wire 2, I₂ = 8 A
distance between two conductors, r = 10 cm = 0.10 m
Let, x be the distance of third wire from wire 1, then 0.10 - x is the distance of the third wire from wire 2.

Force on third wire due to wire 1 is, \[F_1 = \frac{\mu_0 I_1 I}{2 \pi x}\] where I is the current flowing through the third wire. Similarly, force on third wire due to wire 2 is, \[F_2 = \frac{\mu_0 I_2 I}{2 \pi (0.10 - x)}\]
The third wire experiences zero force if this two forces are equal.
\[\begin{align*} F_1&=F_2\\ \frac{\mu_0 I_1}{2 \pi x}&=\frac{\mu_0 I_2}{2 \pi (0.10-x)}\\ \frac{12}{x}&=\frac{8}{0.10-x}\\ 0.3 - 3x&=2x\\ \therefore x&=0.06 m\\ \end{align*}\]
Conclusion: The third wire must be placed at a distance 0.06 m from the first wire.

An electron of K.E. 10 eV is moving in a circular orbit of radius 11 cm, in a plane at right angles to a uniform magnetic field. Determine the value of the flux density. (mass of an electron = 9.1×10^-31 kg, e = 1.6×10^-19 C).
Solution:
K.E. = 10 eV = 10×1.6×10^-19 J = 16×10^-19 J
radius, r = 11 cm = 0.11 m
mass of electron, m = 9.1×10^-31 kg
charge of electron, e = 1.6×10^-19 C

For an electron to move in a circular orbit, the force due to magnetic field should be equal to the centripetal force.

\[Bev =\frac{mv^2}{r}\] Now, \[\begin{align*} K.E.& =\frac{mv^2}{2}\\ 16 \times 10^{-19}&=\frac{1}{2} \times 9.1 \times 10^{-31} \times v^2\\ v&= 1.9 \times 10^6 \hspace{0.1cm} m/s\\ \end{align*}\] Then, \[\begin{align*} Bev&=\frac{mv^2}{r}\\ B&=\frac{mv}{er}\\ &=\frac{9.1 \times 10^{-31} \times 1.9 \times 10^6}{1.6 \times 10^{-19} \times 0.11}\\ \therefore B&=9.7 \times 10^{-5} \hspace{0.1cm} T\\ \end{align*}\]

Conclusion: The flux density is 9.7×10^-5 T.

A copper wire 28 m long is wound into a flat circular coil 8.0 cm in diameter. If the current of 4.50 A flows through the coil, what is the magnetic induction at the centre?
Solution:
length, l = 28 m
diameter of circular coil, d = 8.0 cm
radius of circular coil, r = 4.0 cm = 4.0×10^-2 m
current, I = 4.50 A
magnetic induction at the centre, B = ?
Since there are n number of turns in length l , it is found that, \[\begin{align*} n \times 2\pi r&=l\\ n \times 2 \pi \times 4.0 \times 10^{-2} & = 28\\ \therefore n&=111 \hspace{0.1cm} \text{turns}\\ \end{align*}\]
Now, \[\begin{align*} B&=\frac{\mu_0 n I}{2r}\\ &=\frac{4\pi \times 10^{-7} \times 111 \times 4.50}{2\times 4.0 \times 10^{-2}}\\ \therefore B&= 7.8\times 10^{-3} \hspace{0.1cm} T\\ \end{align*}\]

An alpha particle makes a full rotation in a circle of radius 1.0 meter in 2.0 sec. Calculate the value of magnetic field induction at the center of the circle. (μ₀ = 4π ×10^-7 H/m)
Solution:
For an alpha particle,
charge, q = 2e
radius of circular orbit, r = 1.0 m
time, T = 2.0 sec
magnetic induction, B = ?

Now, \[\begin{align*} I&=\frac{q}{T}\\ &=\frac{2e}{T}\\ &=\frac{2 \times 1.6 \times 10^{-19}}{2.0}\\ \therefore I&=1.6 \times 10^{-19}\hspace{0.1cm} A\\ \end{align*}\]
Then, \[\begin{align*} B&=\frac{\mu_0 I}{2r}\\ &=\frac{4\pi \times 10^{-7} \times 1.6 \times 10^{-19}}{2 \times 1.0}\\ \therefore B&=1.00 \times 10^{-25} \hspace{0.1cm} T\\ \end{align*}\]
Conclusion: The required value of magnetic field induction at the center of the circle is 10^-25 T.

A coil consisting of 100 circular loops with radius 0.60 m carries a current of 5 A. At what distance from the center, along the axis, the magnetic field magnitude 1/8 as great as it is at the center?
Solution:
number of turns, n = 100
radius, a = 0.60 m
current, I = 5 A
distance from the center, x = ?
At x , the magnetic field be B' and B be the magnetic field at the center of the coil.

Now, \[\begin{align*} B'&=\frac{B}{8}\\ \frac{\mu_0 I a^2}{2(a^2+x^2)^{3/2}}&=\frac{\mu_0 I}{8 \times 2a}\\ \frac{0.60^2}{2(0.60^2 + x^2)^{3/2}}&=\frac{1}{16\times 0.60}\\ \therefore x&=1.08 \times 10^{-4}\hspace{0.1cm} m \hspace{0.1cm} \text{Solve this!}\\ \end{align*}\]

Conclusion: The required distance is 1.08×10^-4 m.
Last updated on 15^th September, 2022.