The driver cell of a potentiometer has an emf of 2 V and negligible internal resistance. The potentiometer wire has a resistance of 3 Ω. Calculate the resistance needed in series with a wire if a p.d. 5.0 mV is required across the whole wire. The wire is 100 cm long and a balanced length of 60 cm is obtained for a thermocouple of emf E. What is the value of E?

The driver cell of a potentiometer has an emf of 2 V and negligible internal resistance. The potentiometer wire has a resistance of 3 Ω. Calculate the resistance needed in series with a wire if a p.d. 5.0 mV is required across the whole wire. The wire is 100 cm long and a balanced length of 60 cm is obtained for a thermocouple of emf E. What is the value of E?
Solution:

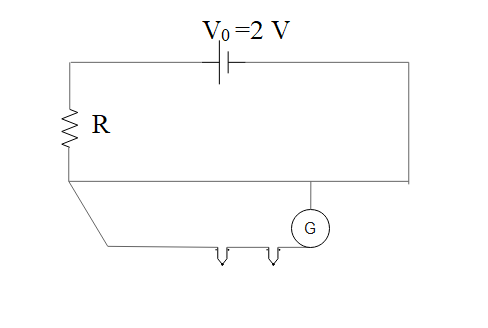
emf of driver cell, \(V_0\) = 2 V
resistance of potentiometer wire, \(R_{AB}\) = 3 Ω
resistance to be connected in series, \(R\) = ?
p.d. across AB, \(V\) = 5 mV = 5 × 10 ^-3
length of potentiometer wire, \(L\) = 100 cm
balancing length for thermoemf , \(l\) = 60 cm
thermoemf, \(E\) = ?
Note that! For the first case just look at the upper section of the figure and for the next part you have to consider the thermocouple (indicted by V in the diagram) that generates thermoemf E.
For first part,
Since \(R\) and \(R_{AB}\) are in series, the total resistance in the circuit is, \[R_T=R+3\] Now, \[\begin{align*} V_0&=I(R+3)\\ I&=\frac{V_0}{R+3}\\ \end{align*}\] Again, \[\begin{align*} V&=I \times R_{AB}\\ 5 \times 10^{-3}&=\frac{V_0}{R+3} \times 3\\ 5 \times 10^{-3} R + 15 \times 10^{-3} &=6\\ R&=1197 \hspace{0.1cm} \Omega\\ \end{align*}\]
For second part,
\[\begin{align*} \text{p.d. across l}&=k l\\ E&=\frac{V_0}{L}\times l \because \text{p.d. across wire = E (for balancing length)}\\ E&=\frac{5 \times 10^{-3}}{100} \times 60\\ \therefore E&=3 \times 10^{-3} \hspace{0.1cm} V\\ \end{align*}\] Hence, the value of E is 3mV .