Elasticity | Complete notes | Important questions | Short questions and Numerical problem solutions | Class 11 (Physics) | Physics in Depth

Elasticity

Structure of a material

Matter is made up of molecules and atoms. The forces between different atoms are responsible for the structure of a molecule and the forces between the molecules are responsible for the structure of the material.

Interatomic and intermolecular forces

The force between two atoms are called the interatomic forces and the force that exists between two molecules are called the intermolecular forces. The potential energy curve is same for atoms and molecules as the force between two atoms has the same general nature as between the two molecules. This is shown in fig. below. The horizontal axis in potential energy curve represents the separation between the atoms / molecules. The zero of the potential energy is taken when the atoms are widely separated (r = infinity). As the separation is decreased from a larger value, the potential energy also decreases, becoming negative. This shows that the force between the atoms / molecules is attractive in this range. As the separation is decreased to a particular value \(r_0\), the potential energy is minimum. At this separation, the force is zero and the atoms can stay in equilibrium. If the separation is further decreased, the potential energy increases.This means a repulsive force acts between the atoms at small separations.
Summary :

• At large separation, \(r>r_0\), the force between two atoms / two molecules is weak and attractive.
• The force increases as the separation is decreased to a particular value and then decreases to zero at \(r=r_0\).
• If the separation is further decreased, \(r < r_0\), the force becomes repulsive.

Elasticity

When external forces are applied, the body may get deformed. When deformed, internal forces develop which try to restore the body in its original shape. The property of a body to restore the natural shape or to oppose the deformation is called elasticity. If a body completely gains its natural shape after the removal of the deforming forces, it is called a perfectly elastic body. A quartz fibre is the nearest approach to the perfectly elastic body. If a body remains in the deformed state and does not even partially regain its original shape after the removal of the deforming forces, it is called a perfectly inelastic or plastic body. Paraffin wax, wet clay are the nearest approach to a perfectly plastic bodies.

Stress

To counteract the deforming force acting on a body, the restoring force is developed within a body which tries to restore the original shape / configuration of the body. The restoring force per unit area of the body is called stress . Remember! Restoring force is equal and opposite to te deforming force. So, stress can also be defined as the deforming force per unit area of the body. \[\begin{align*} \text{stress}&=\frac{\text{external force or deforming force}}{\text{area of the body}}\\ &=\frac{F}{A} \end{align*}\] The SI unit of stress is N/m².

Types of stress

Normal stress

If the external force is applied normally to the surface of a body, then the stress setup in a body is called the normal stress . It is divided into two categories:

Tensile stress

If there is increase in the length of a body in the direction of the applied force, then the stress setup is called the tensile stress as in figure.

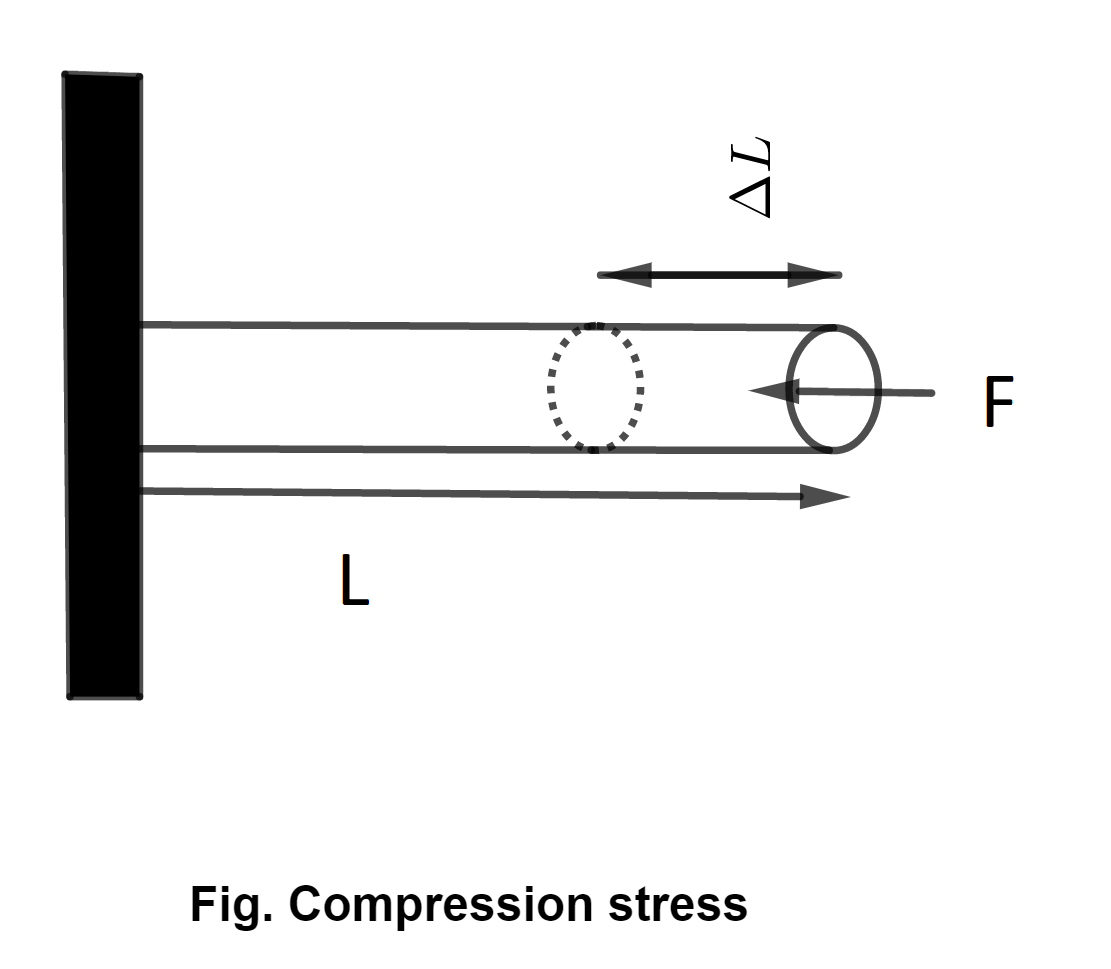
Compression stress

If there is decrease in the length of a body due to the force applied, then the stress setup is called the compression stress as in figure.

A load of 4.0 kg is suspended from a ceiling through a steel wire of radius 2.0 mm. Find the tensile stress developed in the wire.
Here, tension in the wire is, \[F=mg=4\times 10=40 \hspace{0.1cm} \text{N}\] The area of cross section is, \[\begin{align*} A&=\pi r^2\\ &=\pi (2.0\times 10^{-3})^2\\ &=4\pi\times 10^{-6} \hspace{0.1cm} m^2 \end{align*}\] Then, the tensile stress is, \[\begin{align*} &=\frac{F}{A}\\ &=\frac{40}{4\pi\times10^{-6}}\\ &=3.2 \times 10^6 \hspace{0.1cm} N/m^2 \end{align*}\]

Tangential stress or shearing stress

When two equal and opposite forces act tangent to the surfaces of the opposite faces of an object, then one face of the object is displaced with respect to the other face as in fig. .

The shear stress or tangential stress is defined as the shear force per unit area on the face AB (or CD). Since the force along CD is F in magnitude, it forms a couple with the force F applied to the upper side AB. So, the shear stress has a turning or displacement effect owing to the couple present. The solid does not collapse because in a strained equilibrium position such as A'B'CD as in fig., the external couple acting on the solid due to the forces F is balanced by an opposing couple due to stresses inside the material.
Tangential stress or shearing stress is defined as, \[=\frac{F}{A}\]

How much force is required to punch a 1 cm hole in diameter in a steel sheet 5 mm thick whose shearing strength is \(2.76\times10^8 \hspace{0.1cm}Nm^{-2}\).
Here,
radius of hole, r = \(\frac{1}{2}\times 10^{-2}\)m, thickness of steel sheet, d = \(5\times 10^{-3}\) m, shearing strength, S = \(2.76\times 10^8 \hspace{0.1cm}Nm^{-2}\), force required to punch hole, F= ?
The shear stress in the material is, \[=\frac{F}{A}\] The material fails (or hole is punched) when, \[\frac{F}{A}\geq S\] Then,using the above condition, the minimum force to punch the hole in the steel sheet is, \[\begin{align*} F&=S\times A\\ &=2.76\times 10^8\times 2\pi r d\\ &=2.76\times 10^8\times 2\pi \times 0.5\times 10^{-2}\times 5 \times 10^{-3}\\ \therefore F&=43353.97 \hspace{0.1cm} \text{N} \end{align*}\]

Bulk stress or volume stress or hydraulic stress

When a small solid body is immersed in a fluid, (a) the force at any point is normal to the surface and (b) the magnitude of the force on any small surface area is proportional to the area. The body is then said to be under a stress called a bulk stress or volume stress or hydraulic stress .
Bulk stress is defined as,\[=\frac{F}{A}\]

Strain

The ratio of the change in configuration (i.e., shape, length or volume) to the original configuration of the body is called strain.
i.e., \[\text{strain}=\frac{\text{change in configuration}}{\text{original configuration}}\] Strain has no unit and dimensions as it is the ratio of two similar quantities.

Types of strain

Longitudinal strain

The longitudinal strain is defined as the change in length per unit original length produced under the action of the deforming force. If L is the original length of the body and \(\Delta L\) is the change in length, then,
\[\text{longitudinal strain}=\frac{\Delta L}{L}\]

Volumetric strain

The volumetric strain in a body is defined as the change in volume per unit original volume of the body produced under the action of the deforming force. If V is the original volume of the spherical body and \(\Delta V\) is the change in volume, then, \[\text{volumetric strain}=\frac{\Delta V}{V}\]

Shear strain

Shear strain, \(\theta\), is the angular displacement through which the face of the body originally perpendicular to the fixed face is turned when it is under the shearing stress as shown in fig. (see above) . i.e., \[tan\theta=\frac{x}{L} \implies \theta=\frac{x}{L} \hspace{0.1cm} \text{for small}\hspace{0.1cm}\theta, tan\theta \approx \theta\]

Hooke's Law

Hooke's law states that the restoring force acting on a body is directly proportional to extension produced within elastic limit ( Don't worry! I will talk about this very soon).
i.e., \[F \propto x\] \[-F=kx\] Here, x is the extension produced on a body and k is the force constant or spring constant.

Hooke's law can also be stated as, "For the small deformation, the stress produced on a body is proportional to the corresponding strain." i.e., \[\begin{align*} \text{stress} &\propto \text{strain}\\ \text{stress}& = E \times \text{strain} \\ E&=\frac{\text{stress}}{\text{strain}} \end{align*}\] Here, E is the constant of proportionality which is called modulus of elasticity of the material. Its value depends up on the material and on the type of deformation involved.

Proportional limit and Elastic limit

When the strain is small, the stress is proportional to the strain i.e., Hooke's law is valid . The point upto which the stress and strain are proportional is called the Proportional limit.
If the strain is increased a little bit, the stress is not proportional to the strain. However, the wire still remains elastic. The point upto where this behaviour is seen is called the elastic limit .

Stress - Strain curve

If we subject a wire to gradually increasing stress and plot a graph between the stress applied and the corresponding strain produced, we obtain the curve of the form shown in figure, called the stress - strain curve.

Interpretation of the curve :

• There is a linear relationship between stress and strain, i.e., Hooke's law is fully obeyed and thus the wire is perfectly elastic upto the point A. The tensile stress corresponding to A thus gives the proportional limit of the material of the wire.
• Beyond the proportional limit A, Hooke's law doesnot obey i.e., strain increases more rapidly with stress than warranted by the Hooke's law . This is shown by the part AB of the curve. Now, the increase in length of the wire is partly elastic and partly plastic (i.e., if the stress is removed just beyond the point B, the wire does not recover its original condition).
• Beyond the point B, there starts a large but irregular increase in strain upto D with little or no increase in stress. This point B, is called the yield point or elastic limit .
• Beyond the point D, the yielding comes to stop and any further extension in the wire can be produced only by increasing the stress. This continues upto point F and beyond F the extension goes on without even adding the load . And, finally at point E, the wire breaks. This point E is called the breaking point or fracture point .

Types of Moduli of Elasticity

Elastic modulus is the measure of the resistance of the material to elastic deformation. Correponding to the different types of strain, we have the following types of elasticity:

Young's modulus of elasticity

The ratio of normal stress to the longitudinal strain within the elastic limit is called the Young's modulus of elasticity . i.e., \[\text{Young's modulus}, Y=\frac{\text{normal stress}}{\text{longitudinal strain}}\] If F be the force applied normally to a cross sectional area A, such that an increase in length l is produced in an original length L, we have, \[\text{normal stress}=\frac{F}{A}\] and, \[\text{longitudinal strain}=\frac{l}{L}\] So, the Young's modulus of elasticity is, \[\begin{align*} Y&=\frac{\frac{F}{A}}{\frac{l}{L}}\\ Y&=\frac{FL}{Al} \end{align*}\]
A load of 4.0 kg is suspended from a ceiling through a steel wire of length 20 m and radius 2.0 mm. It is found that the length of the wire increases by 0.031 mm as equilibrium is achieved. Find Young modulus of steel.
Here,
mass, m = 4.0 kg , length of wire, L = 20 m , radius, r = \(2.0 \times 10^{-3}\) m, extension of wire, l = \(0.31 \times 10^{-3}\) m, Young modulus, Y =?
Now, the normal stress is, \[\begin{align*} &=\frac{F}{A}\\ &=\frac{mg}{\pi r ^2}\\ &=\frac{4 \times 10}{\pi (2.0 \times 10^{-3})^2}\\ &=\frac{40}{1.26 \times 10^{-5}}\\ &=3.2 \times 10^6 \hspace{0.1cm} \text{Nm}^{-2} \end{align*}\] and the longitudinal strain is, \[\begin{align*} &=\frac{l}{L}\\ &=\frac{0.31\times 10^{-3}}{20}\\ &=1.55 \times 10^{-5} \end{align*}\] Thus, the Young modulus of steel is, \[\begin{align*} Y&=\frac{\text{normal stress}}{\text{longitudinal strain}}\\ &=\frac{3.2\times 10^6}{1.55 \times 10^{-5}}\\ &=2 \times 10^{11} \hspace{0.1cm} \text{Nm}^{-2} \end{align*}\]

Find the maximum load which may be placed on a steel wire of diameter 1.0 mm if the permitted strain must not exceed \(\frac{1}{1000}\) and the Young modulus for steel is \(2.0\times 10^{11}\) Nm\(^{-2}\).
Here,
\[\frac{\text{max. stress}}{\text{max.strain}}=2 \times 10^{11}\] \[\therefore \text{max.stress}=\frac{1}{1000}\times 2 \times 10^{11} = 2\times 10^{8} \hspace{0.1cm} \text{Nm}^{-2}\] Now, area of cross-section, \[A=\pi r^2=\pi \times (0.5 \times 10^{-3})^2=7.85\times 10^{-7} \hspace{0.1cm} \text{m}^2\] and the maximum load is, \[F=\text{stress}\times A=2\times 10^{8}\times 7.85 \times 10^{-7}=157 \hspace{0.1cm} \text{N}\]

Bulk modulus of elasticity

The ratio of normal stress to the volumetric strain, within the elastic limit is called the Bulk modulus of elasticity . i.e., \[\text{Bulk modulus}, K = \frac{\text{normal stress}}{\text{volumetric strain}}\]

If a force F be applied normally and uniformly over the surface of a body, of area A , such that there is change of volume \(\Delta V\) in its original volume V, but no change of shape, we have, \[\text{normal stress}=\frac{F}{A}\] and, \[\text{volumetric strain}=-\frac{\Delta V}{V}\] Here, - ve sign indicates that as the pressure increases, the volume decreases and vice versa.
So, the bulk modulus of elasticity is, \[\begin{align*} K&=\frac{\frac{F}{A}}{\frac{-\Delta V}{V}}\\ K&=-\frac{F}{A}.\frac{V}{\Delta V}\\ K&=-\frac{PV}{\Delta V} \end{align*}\] Here, Increase in pressure applied on the body, \(P=\frac{F}{A}\)

Compressibility : The reciprocal of bulk modulus of elasticity is called compressibility , i.e., \[C=\frac{1}{K}\]

Find the decrease in the volume of a sample of water from the following data: Initial volume = \(1000 \hspace{0.1cm}\text{cm}^3\), initial pressure = \(10^5 \hspace{0.1cm} \text{Nm}^{-2}\), final pressure = \(10^6 \hspace{0.1cm} \text{Nm}^{-2}\), compressibility of water =\(50 \times 10^{-11} \hspace{0.1cm} \text{m}^2\text{N}^{-1}\).
Here,
the change in pressure, \(P=10^6-10^5=9\times 10^5\) Nm\(^{-2}\)
\[\text{compressibility}, C=\frac{1}{K}=-\frac{\Delta V}{PV}\] Then , \[\begin{align*} 50\times 10^{-11}&=-\frac{\Delta V}{9\times 10^5}{10^{-3}}\\ \Delta V&=-50 \times 10^{-11}\times 10^{-3}\times 9\times 10^5\\ &=-4.5 \times 10^{-7} \hspace{0.1cm} \text{m}^3 \end{align*}\] So , the decreae in volume is \(-4.5 \times 10^{-7} \hspace{0.1cm} \text{m}^3\)

Shear modulus or Modulus of rigidity

The ratio of the tangential stress to the shear strain, within the elastic limit is called the Modulus of rigidity . i.e., \[\text{modulus of rigidity}, \eta=\frac{\text{tangential stress}}{\text{shearing strain}}\] Consider the cube as in fig with fixed lower face and a tangential force F be applied on the upper surface whose area is A .

Then, \[\text{tangential stress}=\frac{F}{A}\] Here, the angular displacement \(\theta\) is the shear strain.
So, the modulus of rigidity is, \[\begin{align*} \eta&=\frac{\frac{F}{A}}{\theta}\\ &=\frac{F}{A\theta}\\ &=\frac{F}{A}.\frac{L}{\Delta x}\\ &=\frac{FL}{A\Delta x} \end{align*}\] Here, \(tan\theta \approx \theta=\frac{\Delta x} {L}\)

A cube of aluminium of side 10 cm is subjected to a shearing force of 100 N. The top surface of the cube is displaced by 0.01 cm with respect to the bottom. Calculate the shearing stress, shearing strain and modulus of rigidity.
Here,
Length of each side of cube, L = 10 cm = 0.1m, displacement of top face, l = 0.01 cm = 0.0001 m, area of top face of cube, A = \(l^2=0.1\times 0.1=0.01\)m\(^2\), shearing force, F = 100 N
Now, the shearing stress is, \[=\frac{F}{A}=\frac{100}{0.01}=10^4 \hspace{0.1cm} \text{Nm}^{-2}\] and the strain is, \[\theta=\frac{l}{L}=\frac{0.0001}{0.1}=10^{-3}\] So, the modulus of rigidity is, \[\eta=\frac{\text{shearing stress}}{\theta}=\frac{10^4}{10^{-3}}=10^7 \hspace{0.1cm} \text{Nm}^{-2}\]

Energy stored in a stretched wire or Elastic potential energy of a strained body

When the body is deformed, internal forces appear and work has to be done against these forces. Thus, the potential energy of the body is increased. This is called the elastic potential energy .

Consider that the wire having natural length L and cross-sectional area A is fixed at one end and is stretched by a external force applied on the other end as in fig. (a). If l is the extension of the wire, then \[\text{longitudinal strain}=\frac{l}{L}\] and tensile stress, \[=\frac{F}{A}\] So, the Young's modulus of elasticity, \[\begin{align*} Y&=\frac{\text{tensile stress}}{\text{longitudinal strain}}\\ &=\frac{\frac{F}{A}}{\frac{l}{L}}\\ &=\frac{FL}{Al}\\ F&=\frac{YAl}{L} ... (i) \end{align*}\] The work done by the external force in a further extension (or increase in length) dl is, \[\begin{align*} dW&=F dl\\ &=\frac{YAl}{L} dl \end{align*}\] The total work done by the external force in an extension 0 to l is, \[\begin{align*} W&=\int^l_0 \frac{YAl}{L}dl\\ &=\frac{YA}{L}{l^2}{2} \hspace{0.1cm} \because \int x dx=\frac{x^2}{2}\\ &=\frac{1}{2}\frac{YAl}{L}l\\ &=\frac{1}{2} F\times l \end{align*}\] Thus, the elastic potential energy of the stretched wire ( U ) is, \[=\frac{1}{2}\left( \text{maximum stretching force}\times \text{extension}\right) ... (ii)\] Equation (ii) can also be written as, \[=\frac{1}{2}\frac{Yl}{L}\frac{l}{L}(AL)\] Here, \(\frac{Yl}{L}\) = stress, \(\frac{l}{L}\) = strain and \(AL\) = volume
So, Potential energy = \(\frac{1}{2}\) \(\times\) stress \(\times\) strain \(\times\) volume
Thus, Potential energy per unit volume = \(\frac{1}{2}\) \(\times\) stress \(\times\) strain

A steel wire of length 2.0 m is stretched through 2.0 mm. The cross-sectional area of the wire is 4.0 mm\(^2\). Calculate the elastic potential energy stored per unit volume of the wire in the stretched condition. Young modulus of steel = \(2.0 \times 10^{11}\) Nm\(m^{-2}\).
Here,
length of wire, L = 2.0 m , extension of the wire, l = \(2.0\times 10^{-3}\) m, area of wire, A = \(4.0\times 10^{-6}\) m\(^2\), potential energy per unit volume = ?
strain in the wire is, \[\frac{l}{L}=\frac{2.0 \times 10^{-3}}{2}=10^{-3}\] We have, \[\begin{align*} Y&=\frac{\text{stress}}{\text{strain}}\\ \text{stress}&=Y \times \text{strain}\\ &=2\times 10^{-11} \times 10^{-3}\\ &=2 \times 10^8 \hspace{0.1cm} \text{Nm}^{-2} \end{align*}\] The elastic potential energy per unit volume is, \[\begin{align*} &=\frac{1}{2}\times {\text{stress}} \times {\text{strain}}\\ &=\frac{1}{2} \times 2 \times 10^8 \times 10^{-3}\\ &=10^5 \hspace{0.1cm} \text{J/m}^3 \end{align*}\]

Poisson's ratio

When a deforming force is applied on a wire, it becomes longer but thinner . Thus there occurs the longitudinal as well as lateral strain.
Longitudinal strain, \(\alpha\), is the change in dimensions per unit original dimension along which the force is applied. Lateral strain, \(\beta\), is the change in dimension per unit original dimension in the perpendicular direction (i.e., along the diameter of a wire ).
It has been found experimentally that, \[\begin{align*} \beta &\propto \alpha\\ \beta&=\sigma \alpha\\ \sigma&=\frac{\beta}{\alpha} \end{align*}\] Poisson's ratio is a unitless and dimensionless quantity. Larger the Poisson's ratio, softer is the material.

Elastic after Effect

Solids, in general, takes appreciable time to recover their original condition. The delay in recovery on removal of the deforming force is known as elastic after effect .

Elastic Fatigue

Elastic body subjected to repeated alternating deforming forces for a long period of time gets tired or fatigued. This phenomenon is known as elastic fatigue .

Why are bridges declared unsafe after long use?
The bridges after subjected to alternate cycle of stress and strain gets tired or fatigued. Because of this, the elastic property of the bridge changes and hence for a given stress large strain will be produced thereby increasing the chance of collapse of bridge. Due to this reason, the bridge is declared unsafe after long use.

Elastic hysteresis

When a material is subjected to a full cycle of increasing and decreasing load, the strain is found to be greater for the same value of the stress when it is being unloaded than when it is being loaded, as shown in fig. . The lagging behind of strain is called elastic hysteresis .

Click on Elasticity_questions to find the important questions.
Click on Elasticity_solutions to find the solutions to short questions and numerical problems.