Rotational Dynamics

Rigid body

A rigid body is defined as a solid body in which the particles are compactlt arranged so that the inter-particle distance is small and fixed and is not disturbed by any external forces applied. Such a body thus does not bend, stretch or vibrate when in motion. No ideal rigid-bodies exist! but the bodies, in which the small forces required to move them produce little or no bending, stretching etc., may be taken to be rigid.

Translation and Rotation

When a rigid body move as a whole in any direction, then the body is said to be in translatory motion. However, when a body turns around or rotate about a particular axis, then the body is said to be in rotational motion. A body may execute both translational and rotational motion simultaneously (at the same time) .
Pure rotation: Consider the ceiling fan in your room. When it is on, each point on its body goes in a circle. Locate the centres of the circles traced by different particles on the three baldes of the fan and the body covering the motor. All these centres lie on a vertical line through the centre of the body (i.e., axis of rotation ). The fan rotates about this axis of rotation. Here, the centre of the fan (center of mass) remains unmoved, and the fan is said to have a pure rotational motion.

Fig. Pure rotatory motion
Image Source: gifer.com Pure translation : Consider the block of metal sliding down the inclined plane as in fig. In this case, every point on the metal block moves with the same velocity equal to the linear velocity of centre of mass 'O' i.e., v . Here, the block is said to have pure translational motion.

Pure rolling ( combined rotation and translation ): Consider cycling a bicycle on the road. After one full pedal, the wheel covers certain distance (i.e., 2πR (R is the radius of wheel)). This type of motion of of a wheel (or any other oject with circular boundary) in which the centre of wheel moves in a straight line and the wheel rotates in its plane about its centre is called pure rolling .

Moment of inertia

At first, let's try to understand the inertia in case of linear or translatory motion. Inertia is the inability of a body to change itself its state or rest or uniform motion along a straight line. In other words, inertia is the tendency of a body to resist acceleration. It is an inherent property of a matter. The greater the mass of a body, the greater the resistance offered by it to any change in its state of rest or linear motion . In other way, it means the more mass the body has, the more resistance to the acceleration the body offers. So, mass is taken to be the measure of inertia for linear or translatory motion. Let's look at this in some more detail. Don't worry! we will return to the topic (i.e., moment of inertia ) very soon! Take a chair and a table. It is easier to accelerate chair than the table because chair has larger mass and thus larger inertia. Object with larger inertia will have larger resistance to acceleration. Hope, It's clear to you now. Let's now move to our topic!

In exactly manner, a body free to rotate about an axis opposes any change in its state of rest or uniform motion. In other words, it possesses inertia for rotational motion i.e., it opposes the torque or the moment of couple applied to it to change the state of rotation. This property of a body is called the moment of inertia .
Mathematically, the moment of inertia of the rigid body is,
\(I=\sum_{i=1}^{n} m_i r_i^2\) Here, \(m_i\) is the mass of the \(i^{th}\) particle of rigid body and \(r_i\) is the perpendicular distance of that particle from the axis of rotation as in fig. The S.I. unit of moment of inertia is kgm².

Understanding the Moment of Inertia Rotate a long, fairly heavy rod (a pole, or something similar), first around its central (longitudinal) axis as in Fig. (a) and then around an axis perpendicular to the rod and through the centre as in Fig. (b) Both rotations involve the very same mass, but the first rotation is much easier than second. Why? . The reason is that the mass is distributed much closer to the rotation axis in the first rotation. Thus, the rotational inertia of the rod is much smaller in Fig. (a) than Fig. (b). Smaller rotational inertia or moment of inertia means easier rotation.

Theorem of parallel axis: The moment of inertia of inertia of a body about any axis is equal to its moment of inertia about a parallel axis through its centre of mass plus the product of the mass of the body and the square of the distance between the two axes.
I=I_cm+Mr² here, I_cm is the moment of inertia about the parallel axis through its centre of mass, M is the total mass of the body and r is the distance between the two axes.

Theorem of perpendicular axis: The sum of moment of inertia of a laminar body ( a two-dimensional planar closed surface ) about any two mutually perpendicular axes in its plane is equal to its moment of inertia about an axis perpendicular to its plane and passing through the point of intersection of the two axes.
I_x+I_y=I_z

Moment of inertia of different rigid bodies

Thin uniform rod (about an axis through its centre): \(I=\frac{Ml^2}{12}\)
Thin uniform rod (about an axis passing through one end and perpendicular to its length): \(I=\frac{Ml^2}{3}\)
Circular ring (about an axis through its centre and perpendicular to its plane): I=MR²
Circular ring (about its diameter): \(I=\frac{MR^2}{2}\)
Thin circular disc (about an axis through its centre and perpendicular to its plane): \(I=\frac{MR^2}{2}\)
Thin circular disc (about a diameter): \(I=\frac{MR^2}{4}\)
Rectangular lamina or bar or plate (about an axis through its centre and perpendicular to its plane): \(I=\frac{M(l^2+b^2)}{12}\) ; l and b are sides or rectangle.
Solid cylinder (about its own axis of cylindrical symmetry): \(I=\frac{MR^2}{2}\)
Solid sphere (about a diameter): \(I=\frac{2}{5}MR^2\)

Radius of gyration

The moment of inertia of an object ∑ mr² is sometimes written as MK² where M is the mass of the object and K is a quantity called the radius of gyration . For example, moment of inertia of solid sphere about its diameter is , \(I=\frac{2}{5}MR^2\). Thus the radius of gyration is , \(K=\sqrt{\frac{2}{5}R^2}=\sqrt{\frac{2}{5}} R\).
Radius of gyration of a body about its axis of rotation is the effective distance of its particles from the axis.It is actually that distance from the axis at which if its entire mass (M) be supposed to be concentrated, its moment of inertia about the given axis would be same as with its actual distribution of mass.

Torque on a rotating body

Image source: scienceabc.com
Torque (Latin; 'to twist') is defined as the turning or twisting action of the force in a body. Mathematically,
\(\tau=\vec{r} \times \vec{F}\) The magnitude of torque is,
τ=rF Here, r is the perpendicular distance between the rotation axis and line of action of \(\color{red}\vec{F}\) ( extended line through the vector \(\vec{F}\)) as in figure.

If the body rotates in clockwise direction, then the torque applied on the body is said to be clockwise torque . However, if the body rotates in anti-clockwise direction, then the torque applied on the body is said to be anti-clockwise torque .
Torque is measured in Newton-metre (Nm) and is often confused with work (same unit). However, these two quantities are entirely different. Work is often expressed in Joules but torque never is.

Direction of torque

Right hand thumb rule gives the direction of torque. Sweep your fingers of the right hand from \(\vec{r}\) into \(\vec{F}\), the outstreched right thumb then gives the direction of torque.

Relation between torque and moment of inertia

You use a torque to a rotate a body (e.g., a door) . We can relate the torque to angular acceleration (α) . By analogy with Newton's second law of motion (F = ma), we replace m by I and a by α with result,
τ = Iα
This relation is sometimes referred as Newton's second law for rotation . Angular acceleration (α) is rotational analogy of linear acceleration (a) and is the rate of change of angular velocity (ω).

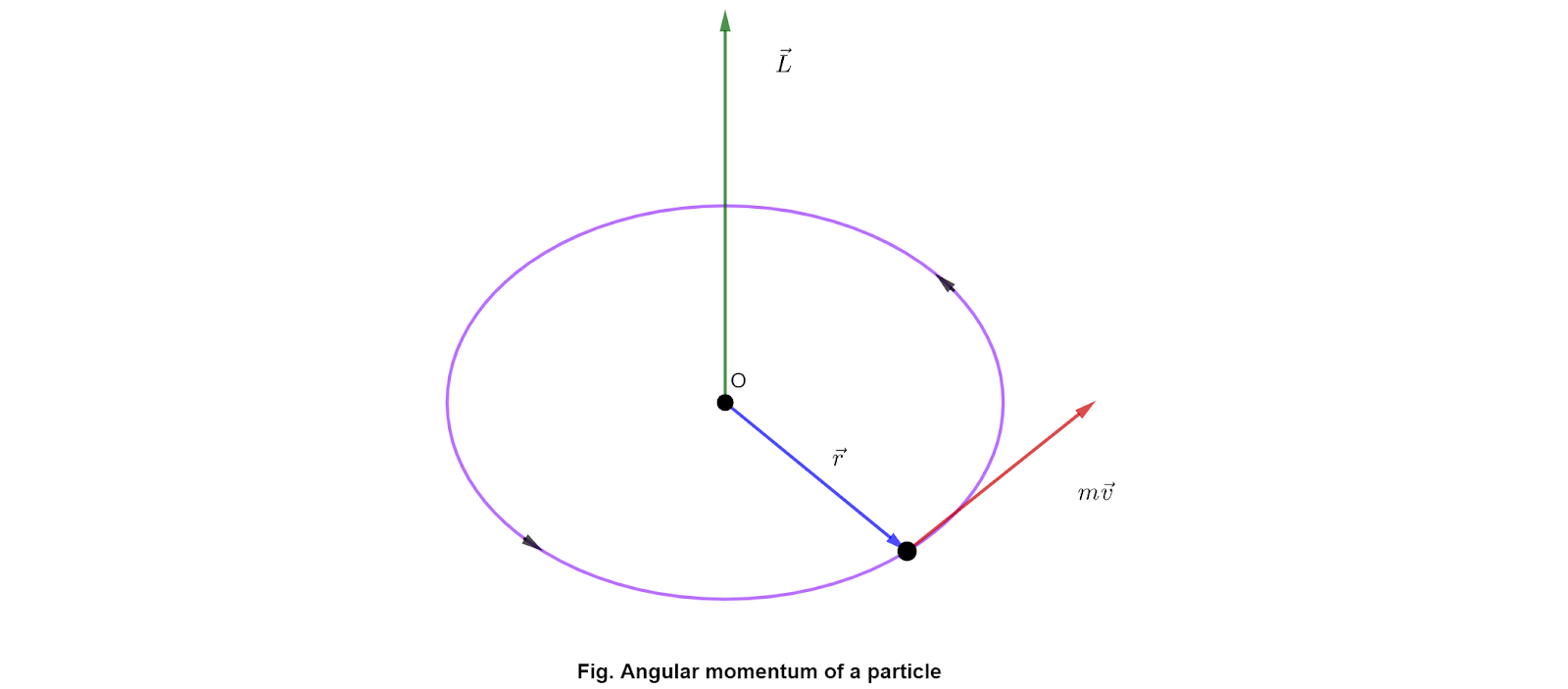
Angular momentum

The angular momentum \(\vec{L}\) of the particle with mass m, linear momentum p with respect to the origin O is ,
\(\vec{L}=\vec{r}\times \vec{p}\) Here \(\vec{r}\) is the position vector of the particle with respect to O. It is also called the moment of linear momentum . Angular momentum of rotational analogy of linear momentum. The magnitude of angular momentum is,
L = rp = mvr \(\because\) p = mv Here, r is the perpendicular distance from the axis or rotation to the direction of momentum of a body.Since, v=rω, L=mr²ω. The S.I. unit of angular momentum is kg m²/s (or Js) and it is a vector quantity.

Relation between angular momentum and moment of inertia

L = Iω

Relation between angular momentum and torque

\(\tau=\frac{dL}{dt}\) It is analogous to \(F=\frac{dp}{dt}\) (Newton's second law of motion) and hence is sometimes called as Newton's second law in angular form . It can be stated as, the net torques acting on a particle is equal to the time rate of change of angular momentum of that particle.

Conservation of Angular momentum

If no external torque acts on a system, the angular momentum of the system remains constant, no matter what changes takes place within the system. i.e., if for \(\tau\) = 0, \(\frac{dL}{dt} = 0 \implies\) L=constant.
L = Iω = constant This means,
total angular momentum at some initial time = total angular momentum at some later time ; (in absence of external torque)
If I₁ , ω₁ be the initial and I₂ , ω₂ be the final moment of inertia and angular velocity respectively, then, from the conservation of angular momentum,
I₁ω₁ = I₂ ω₂

Examples

When a high diver jumps from a diving board, his moment of inertia can be decreased by curling his body more (since, decreasing r decreases moment of inertia, I = mr²), in which case his angular velocity ω is increased (Iω = constant). He may then be able to take more somersaults before striking the water.

Fig. As the diver jumps from the board, her angular velocity can be increased by curling her body

Image source: tutorials point

When the ballet-dancer stretches her hands and legs outwards, her moment of inertia increases and thus the angular velocity decreases (Iω = constant). When she wants to increase her spinning rate, she brings her arms and legs closer reducing the moment of inertia which thus increases the angular velocity.

Image Source: The Physics of Dance

What happens to the time period of rotation of earth or how will the length of day be affected on earth if it is struck by meteorites?
The earth rotates about an axis passing through its geographic north and south poles with a period of 1 day. If it is struck by meteorites, since action and reaction are equal , no external couple (torque) acts on the earth and meteorites and thus the angular momentum is conserved.
angular momentum of earth plus meteorites after collision = angular momentum of earth before collision Here, we have neglected the angular momentum of the meteorites about the earth axis before collision compared with that of earth. Since, the effective mass of the earth has increased after the collision the moment of inertia ( I = mr²) has increased. So, the earth will slow down (Since, L=Iω) slightly. Note! In this case, increase in I has decreased ω so that L remains constant (i.e., conserved).
Due to the decrease in \(\Omega\), time period of rotation of earth increases which thus increases the length of the day.

Work done by a couple

The result for the work done by a couple is,
work done by a couple = torque × θ
where, θ is the angle of rotation and is always expressed in radians. Suppose, F = 20 N, r = 0.4 metre, and the wheel makes 5 revolutions while the torque is kept constant. Then from above,
torque = 20 × 0.08 (τ = rF)
and
angle of rotation = 2π × 5 radian
∴ work done = 20×0.08×2π×5 = 50 J

Kinetic energy of a rotating body

The rapidly rotating blade of a ceiling fan certainly has kinetic energy due to that rotation. Can we express that energy as K.E.=½ mv²
? NO! . Because this equations deals with the motion of center of mass of ceiling fan which is actually zero ( already discussed!) in pure rotation. So, to describe the kinetic energy of rotating body, we use the relation,
K.E.=½ Iω² As in the previous cases, you can find the analogy between translational kinetic energy and rotational kinetic energy. I leave it to you! Enjoy!

Kinetic energy of a rolling body

When an object such as a cylinder or ball rolls on a plane, the object is rotating as well as moving down the plane. So, it has rotational K.E. in addition to the translational K.E. . So,
total kinetic energy = ½ mv² + ½ Iω²

Acceleration of a rolling body on an inclined plane

Consider a uniform cylinder or a disc or a sphere, etc. C rolling along a inclined plane without slipping as in fig. below. r be the radius of the rolling body, I be the moment of inertia about the axis O, ω be the angular velocity about O and v =ω R. So,
total kinetic energy = \(\frac{1}{2}Mv^2+\frac{1}{2} I(\frac{v}{r})^2=\frac{1}{2}v^2 \left(M+\frac{I}{r^2}\right)\) Suppose the body rolls from rest through a distance s along the plane, then from the figure, we find that h=s sinθ and the loss in potential potential energy is thus, mgs sinθ (i.e., mgh). Here,
Loss in P.E. = Gain in K.E. So,
\(mgs sin\theta= \frac{1}{2}v^2 \left(M+\frac{I}{r^2}\right)\) From this expresion, we can write,
\(v^2=\frac{2mgs sin\theta}{m+\frac{I}{r^2}}\) But, v²=2as (since, u=0), we obtain the expression for a as,
\(a=\frac{mgsin\theta}{M+\frac{I}{r^2}}\)
Solid solid has a greater acceleration down the plane than a hollow cylinder of the same mass. Why?
A uniform hollow cylinder of mass m and radius r has a moment of inertia I=½ mr² about its axis. So, I/r² = m/2. Substituting this in the expression just derived, we find that the acceleration down the plane a=2g sinθ . A uniform hollow cylinder open at both ends has a moment of inertia I=mr². Substituting this, we get the acceleration down the plane as a = g sin(θ/2). So, the solid cylinder would have a greater acceleration down the plane than a hollow cylinder of same mass.

Click on Rotational dynamics_questions to find the important questions.
Click on Rotational dynamics_solutions to find the solutions to short questions and numerical problems.

Physics in Depth