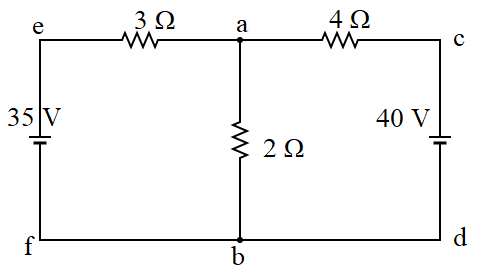
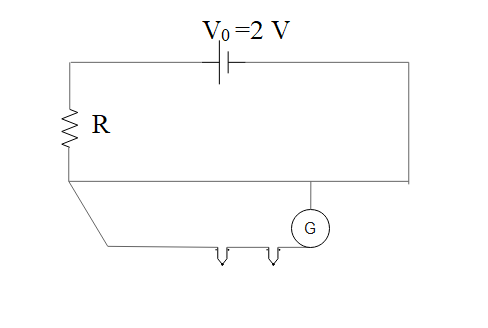
Electrons | Complete notes with short answer questions and numerical problem solutions | Class 12 NEB Physics

Electrons Introduction and background Electron is the lightest subatomic particle. It carries a charge of -1.602176634 × 10 -19 C, which is considered the fundamental or basic unit of electric charge. The mass of an electron is 9.1093837015 × 10 -19 kg which is \(\frac{1}{1836}\) times the mass of a proton (a positively charged constituent of an atom). Discovery of electrons: The discharge tube experiment played an important role in the discovery of electrons. While studying the properties of cathode rays (1897 A.D.), J.J. Thomson ( Nobel prize for Physics, 1906 ) found that the cathode rays are deflected in electric and magnetic fields which led scientists to believe that the cathode rays are made of tiny negatively charged particles. ( Note! In this chapter, we will learn how the electrons get affected by the electric and magnetic fields so you would know why scientists came in conclusion to identify the discovered particle as negatively...