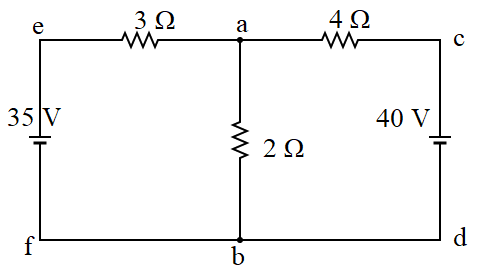
Using Kirchhoff's laws of current and voltage, find the current in 2 Ω resistor in the given circuit.

Using Kirchhoff's laws of current and voltage, find the current in 2 Ω resistor in the given circuit.

Solution:

Using Kirchhoff's junction rule,
At junction a,
\[I_1+I_3=I_2 \hspace{0.1cm} \text{ ... (i)}\] Using Kirchhoff's loop rule,
In loop ecdfe,
\[\begin{align*} -I_1 \times R_1 + I_3 \times R_3 - E_2 + E_1 &=0\\ -I_1 \times 3 + I_3 \times 4 - 40 + 35 &=0\\ 4I_3 - 3I_1&=5 \hspace{0.1cm} \text{ ... (ii)}\\ \end{align*}\] In loop eabfe, \[\begin{align*} -I_1 \times R_1 - I_2 \times R_2 + E_1&=0\\ -I_1 \times 3 - I_2 \times 2 +35 &=0\\ -3I_1 - 2(I_1+I_3)+35&=0\\ -3I_1-2I_1-2I_3+35&=0\\ -5I_1-2I_3+35&=0\\ 5I_1+2I_3&=35 \hspace{0.1cm} \text{ ... (iii)}\\ \end{align*}\] Multiplying equation (iii) by 2 and subtracting (ii) from (iii), we get,
\[\begin{align*} 4I_3+10I_1-70-(4I_3-3I_1-5)&=0\\ 13I_1&=65\\ \therefore I_1&=5 \hspace{0.1cm} A\\ \end{align*}\] Substituting this in equation (ii),
\[\begin{align*} 4I_3-3\times 5&=5\\ \therefore I_3&=5 \hspace{0.1cm} A\\ \end{align*}\] Thus, from equation (i), \[I_2=I_1+I_3 = 10 \hspace{0.1cm} A\] Hence, the current through 2 Ω resistor is 10 A .