Kinematics | Complete notes | Important Questions | Class 11 (Physics) | Physics in Depth
Kinematics
Rest and Motion
When do you declare that some body is in rest or in motion? Place the book on a table and watch it! Is it in rest? Imagine you being on moon and by some means you could watch your book on your table. Would you again see it in rest? In first case, you would see that the book is in rest but when you are on moon you would see the table, the book and the Earth as a whole in a motion. You are correct in both the cases and it's a good news. Hurray!.It is because rest and motion are not absolute terms but are relative. The book is in rest when you see it from your room because you and the book both do not change position with respect to each other, but it is in motion when you see it from the moon because the moon is moving with respect to the book and book moves with respect to the moon.
So, let's set up a definition. If a body changes it's position with respect to the observer ( or reference frame ), then it is said to be in motion with respect to that observer ( or reference frame ). Otherwise, the body is said to be in rest.
When someone says that the car is travelling and motorbike is at rest, it is clear that the frame of reference (with respect to which we locate the position of a body), is attached to the road.
Kinematics
Kinematics is the branch of mechanics that deals with the motion of an object without reference to the forces which cause the motion. It is the classification and comparison of motions. For the measurement and comparison of motion, we restrict ourselves to the three general properties of the motion i) the motion is in a straight- line only i.e., it may be vertical, horizontal, or slanted, but it must be straight. ii) forces that cause motion will not be taken reference into. iii) the moving object is either a particle ( such as an electron i.e., point - like object) or an object that moves like a particle (every portion moves in the same direction at the same velocity).
Displacement
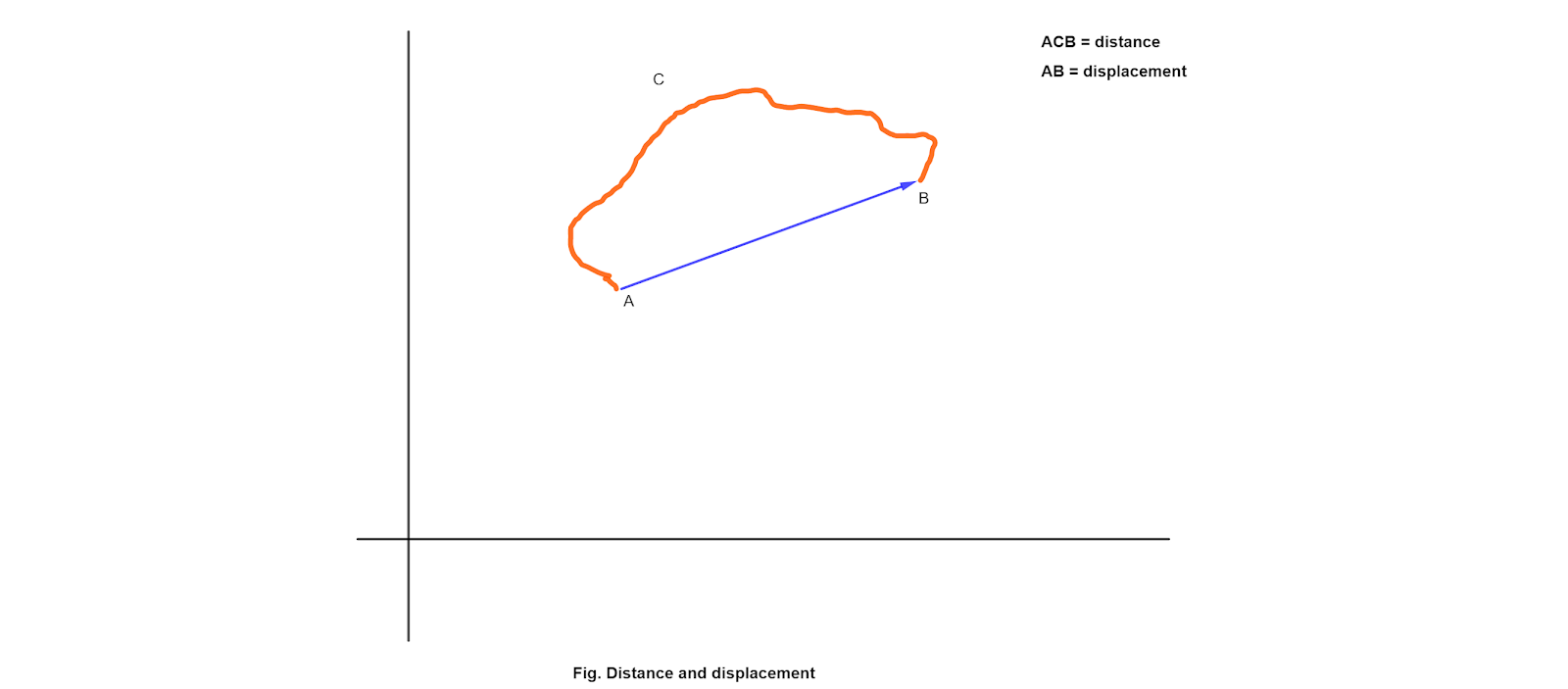
How do you locate an object? To locate an object's position, you need some reference point, Don't you? That reference point is often called as origin ( or zero point ) of an axis such as x-axis, or y-axis, etc. In one dimensional motion, the positive direction is in the direction of increasing coordinates and negative in the opposite direction of this. For example, if one says particle is located at x = 5 m, it means that the particle is 5 m in the positive direction from the origin. If it is in x = -5 m, then it is 5 m in the negative direction from the origin.
Displacement (\(\Delta x\)) is the change of position from position \(x_1\) to the position \(x_2\). \[\Delta x = x_2 - x_1 \]
In 25 min, a man ran 2.40 km on a treadmill facing due east. Relative to the gym, what was his displacement?
Since, the displacement is the change in position of an object, we can unarguably say that the man has 0 displacement as he has not changed his position (\(\Delta x=x_2-x_1\)) relative to the gym.
Average speed and Average velocity
The average speed \(s_{av}\) of an object is the ratio of total distance travelled by the object to the total time interval (\(\Delta t\)) i.e., \[s_{av}={\text{total distance} \over \Delta t}\] It does not indicate direction and hence is scalar quantity.
Average velocity \(v_{av}\) of an object is the ratio of total displacement travelled by an object to the total time interval (\(\Delta t\)) i.e., \[v_{av}={\Delta x \over \Delta t}={{x_2-x_1}\over{t_2-t_1}}\] It is a vector quantity as it indicates the direction.
Distance-time graph
When the distance covered by an object is plotted against the time, it is called the distance-time graph as in fig. This graph does not represent the path followed by an object but it shows the change of position with time. In the fig., the distance-time graph for a running rat is shown. To find the average velocity, first we need to draw a straight line, and find the slope. It is illustrated in fig.
Instantaneous velocity
Average velocity describes how fast an object is moving over a certain interval of time but when it comes to measure how fast the particle is moving at a given instant of time , we measure the instantaneous velocity (or simply velocity) of that object. To obtain the instantaneous velocity from average velocity, the total time interval is shrinked closer to 0 (\(\Delta t \rightarrow 0\)) which approaches a limiting value, which is the instantaneous velocity, \[v={\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{dx}{dt}\]
Acceleration
Acceleration is defined as the rate of change of velocity of a body with respect to time (we have all gone through this same definition again and again from primary schools right?!) . The average acceleration over a time interval (\(\Delta t=t\)) is, \[a_{avg}={\Delta v \over \Delta t}={{v-u} \over {t}}\] Instantaneous acceleration (or acceleration) is the rate of change of velocity of a body at a particular instant of time (\(\Delta t \rightarrow 0\)). Mathematically, \[a=\frac{dv}{dt}\]
Velocity-time graph
When the velocity of an object is plotted against the time, it is called the velocity-time graph. To find the average acceleration from the graph, first we need to draw a straight line, and find the slope. It is illustrated in fig.
Equations of motion
\[v=u+at\] \[v_{av}=\frac{u+v}{2}\] \[s=ut+\frac{1}{2}at^2\] \[v^2=u^2+2as\] If the body is falling freely ( i.e., with an acceleration equal to g ), then we replace \(a\) by \(g\) and \(s\) by \(h\). For the vertically upward motion, \(a = -g\) and \(s=h\).Jump to Relative velocity and Projectile .
Comments
Post a Comment