Kinematics | Relative velocity and projectile motion | Short Questions and Numerical Problem Solutions | Class 11 (Physics) | Physics in Depth

Relative velocity

Relative velocity, \(\vec{v_{AB}}\), is the velocity of an object A in the rest frame of an object B. Rest frame of a particle is the coordinate system (frame of reference) in which the particle is at rest. It can be simply defined as, the velocity of an object with respect to another object . Suppose you are in a car A moving north at 90 km/h (with respect to the object in the ground outside). To another man in a car B moving towards north with same speed, you seem to be stationary. Let's discuss this in more detail. For this, we consider following three cases:

1. When the two bodies, body A and body B, are moving in the same direction with velocity \(\vec{v_A}\) and \(\vec{v_B}\) respectively, then the relative velocity of A with respect to B is, \[\vec{v_{AB}}=\vec{v_A}-\vec{v_B}\] So, in above example, it must be clear that for a person in car B moving alongside you with the same speed as yours, you are at rest.
   
2. When this bodies are moving in opposite direction, then relative velocity of A with respect to B is, \[\vec{v_{AB}}= \vec{v_A}+\vec{v_B}\] So, if in the case of above example, if car B was moving towards south, then to the person in car B, you (in car A) seems to be moving at a speed of 180 km/h.
   
3. When this bodies are moving making an acute angle θ (i.e. acute angle), relative velocity of A with respect to B or B with respect to A is calculated by the rule of vector subraction (click on Physics in Depth to watch the video on vector subtraction). To calculate \(\vec{v_{BA}}\), the direction of \(\vec{v_A}\) should be reversed and the parallelogram is drawn such that the diagonal gives \(\vec{v_{BA}}\) as in fig.

Raindrops hitting the side windows of a car in motion often leave diagonal streaks even if there is no wind. Why?

Let \(\vec{V_r}\) be the velocity of rain and \(\vec{V_c}\) be the velocity of car as in figure. Also, \(\vec{V_{rc}}\) be the relative velocity of rain with respect to car making an angle \(\theta\) with the direction of \(\vec{V_r}\). From figure, we see that, \(\theta=tan^{-1}\left(\frac{V_c}{V_r}\right)\). Since, the relative velocity of rain with repect to rain is directed at an angle \(\theta\) with the vertical velocity or rain, diagonal streaks are often left on the side windows of car.

A man can swim in still water at a speed of 3 km/h. He wants to cross a river that flows at 2 km/h and reach the point directly opposite to his starting point. (a) In which direction should he try to swim (that is, find the angle his body makes with the river flow)? (b) How much time will he take to cross the river if the river is 500 m wide?

Let, \(\vec{v_{rg}} = 2 km/h \) be the velocity of river with respect to ground, \(\vec{v_{mr}} = 3 km/h\) be the velocity of man with respect to river and \(\vec{v_{mg}}\) be the velocity of man with respect to ground and θ be the angle which the man makes with the river flow.
From the fig., \[sin\theta=\frac{v_{rg}}{v_{mr}}\] \[\theta=sin^{-1}\frac{2}{3}\] \[\therefore \theta= 41.8^\circ \] (a) So, the angle made by the swimmer with the direction of river flow is (90+41.8)\(^\circ\)=131.8\(^\circ\).
Also, \[\begin{align*} (v_{mr})^2&=(v_{rg})^2+(v_{mg})^2\\ 9&=4+(v_{mg})^2\\ \therefore v_{mg}&=\sqrt{5} km/h \end{align*} \] (b) Then, the time to cross the river is, \[t=\frac{500}{\frac{\sqrt{5}\times1000}{3600}}=804.98\hspace{0.1cm} s\]

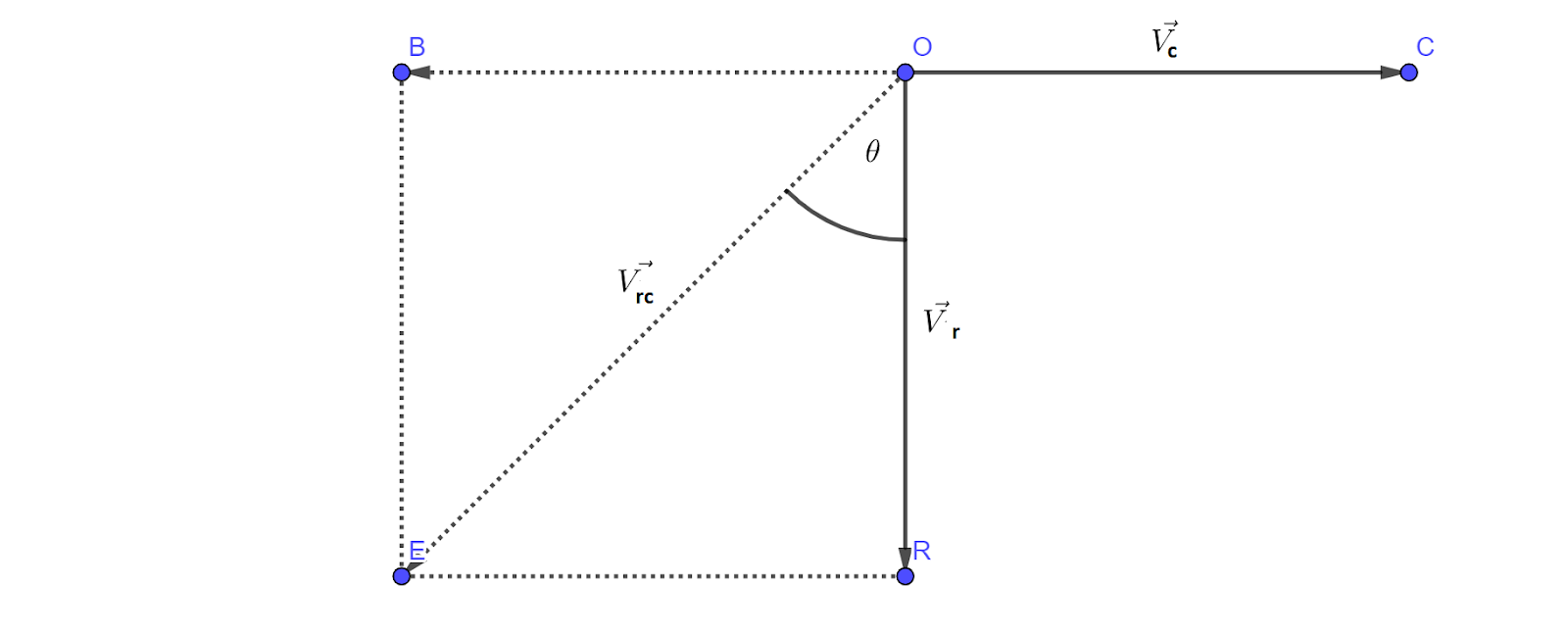
Snow is falling vertically at a constant speed of 8.0 m/s. At what angle from the vertical do the snowflakes appear to be falling as viewed by the driver of a car travelling on a straight, level road with a speed of 50 km/h?
Let, \(v_s=8\) m/s be the speed of snow, \(v_c=50\) km/h be the speed of car and \(v_{sc}\) be the speed of snow with respect to car , making an angle θ with the vertical as in fig..

From the fig., \[tan\theta=\frac{v_c}{v_s}=\frac{\frac{50\times 1000}{3600}}{8}\] \[\theta=tan^{-1} \frac{125}{72}=60.05^\circ\]

A swimmer's speed along the river (down stream) is 20 km/h and can swim up-stream at 8 km/h. Calculate the velocity of stream and the swimmer's possible speed in still water.

speed upstream = speed in still water - speed of stream speed downstream = speed in still water + speed of stream Adding this two , we get, speed upstream + speed downstream = 2 (speed in still water) \[\therefore \text{speed in still water}=\frac{8+20}{2}=14 km/h\] To calculate the speed of stream, use the value of speed in still water in either of two equations above to get 6 km/h.

Projectile

An object thrown into atmosphere so that it falls under the effect of gravity alone is called projectile and its motion is called projectile motyion. The path followed by the projectile is called trajectory. Projectile motion is two dimensional motion i.e., it takes place on a plane. In projectile motion, the horizontal motion (let's say in x-axis) and vertical motion (let's say in y-axis) are independent of each other; i.e., neither motion affects the other (we will discuss this with the example very soon!). The projectile has no horizontal acceleration because the horizontal velocity of projectile is constant throughout the motion. Vertical acceleration is directed vertically downward and is equal to g but it's vertical velocity changes continuously.

Projectile fired at an angle with the horizontal

\[\text{maximum height}, h_{max} = \frac{u^2 sin^2\theta}{2g}\] \[\text{time of flight}, T=\frac{2u sin\theta}{g}\] \[\text{horizontal range},R=\frac{u^2 sin2\theta}{g}\] Maximum value of horizontal range is , \[R_{max}=\frac{u^2}{g}\] because at \(\theta=45^\circ\) , \(sin2\theta=90^\circ=1\) (\(-1\leq sin\theta \leq +1)\)

Two angles of projection are possible for the same horizontal range.
We have for angle of projection θ, \[\text{horizontal range},R=\frac{u^2 sin2\theta}{g}\] If the angle of projection be \(90-\theta\), then \(sin2\theta=sin(180-\theta)\) = \(sin\theta\). So, there is no change in horizontal range if we replace \(\theta\) by \(90-\theta\). Thus, two angles of projection for same horizontal range are \(\theta\) and \(90-\theta\). Will the time of flight be equal at these angles? Think!

Horizontal projectile

\[\text{time of flight}, T=\frac{2h}{g}\] \[\text{horizontal range},R=u\sqrt{\frac{2h}{g}}\]

In projectile motion, the horizontal motion and the vertical motion are independent of each other.
Release two balls from the top your house; one simply and the other horizontally. The balls have the same vertical motion, both falling through the same vertical distance in the same interval of time, \(T=\frac{2h}{g}\). The fact that one ball is moving horizontally while it is falling has no effect on its vertical motion;i.e., the horizontal and vertical motions are independent of each other.

An airplane is flying with a velocity of 90.0 m/s at an angle of 23.0⁰ above the horizontal. When the plane is 114 m directly above a dog that is standing on level ground, a suitcase drops out of luggage compartment. How far from the dog will the suitcase land? You can ignore air resistance.

Let the suitcase attain \(h\) meter vertical height before drop in \(t\) sec, \[\begin{align*} h&=\frac{u^2sin^2 \theta}{2g}\\ &=\frac{(90)^2 sin^2 23}{20} (g=10 m/s^2)\\ &= 61.83 \hspace{0.1cm} m \end{align*}\] total vertical height (H) = 114 + 61.83 = 175.83 m
time to reach the height h is, \[t=\frac{2usin\theta}{2g} \hspace{0.1cm} (\text{remember! time to reach the greatest height is half of time of flight})\] From this, we get, \[t= 3.52 \hspace{0.1cm} s\] Let, T be the time taken by the suitcase to reach the ground from the maximum height (i.e., 175.83 m ), then, \[\begin{align*} H&=\frac{gT^2}{2} \hspace{0.1cm} {\because} s=ut+\frac{1}{2} gt^2\\ 175.83&=\frac{10 {\times} T^2}{2}\\ T^2&=35.17\\ \therefore T&=5.93 \hspace{0.1cm} s \end{align*}\] total time taken by the suitcase to reach the ground , T' = T+t = 9.45 s.
Now, to find how far from the dog the suitcase drops, \[\begin{align*} R&=u_x \times T'\\ &=ucos\theta \times 9.45\\ &=90 \times cos23\times 9.45\\ \therefore R&=782.89 m \end {align*}\] Therefore, the suitcase drops 782.89 m far from the dog.
Click on Kinematics_questions to find the important questions.
Click on Kinematics_solutions to find the solutions to short questions and numerical problems.