Periodic Motion | Complete Notes | Important questions | Short questions and Numerical problem solutions | Class 12 NEB Physics | Physics in Depth
Periodic Motion
When a body repeats its motion after regular time intervals we say it is in periodic motion . The time interval after which the motion is repeated is called the time period. If a body moves to and fro on the same path, it is said to perform oscillations. Every oscillatory motion continues due to the interaction of inertia and elasticity .
Cause of oscillatory motion
When an oscillator is displaced from its postion of equilibrium by application of a force and thus doing work on it, a restoring force comes into play tending to bring it back to its equilibrium position. According to Hooke's Law, this restoring force is proportional to the displacement and depends upon the elasticity of the system. As soon as the restoring force tries to bring the system back to its equilibrium position, the property of inertia opposes this change in velocity. Further, when the system reaches the equilibrium position, it overshoots the mark and moves beyond the mean position again due to inertia of motion . The motion continues till the deforming force due to inertia develops, bring the system to rest. The restoring force again sets the oscillator into motion back towards the equilibrium positon. The total energy is conserved throughout the process.
Simple harmonic motion
If a particle moves to and fro about a mean position in a straight line such that the acceleration is directed towards the mean position and is directly proportional to the displacement
from that position is called simple harmonic motion . Simple harmonic motion is a special type of oscillation and mean position is also called the centre of oscillation .
If x is the displacement produced and a be the accleration of a body in a simple harmonic motion then,
\[a=-kx\]
Here, k is a constant ( Alert! It is not a force or a spring constant!) and negative sign signifies that the accleration is directed
opposite to the motion of the object.
Displacement equation of SHM and Terms associated with SHM
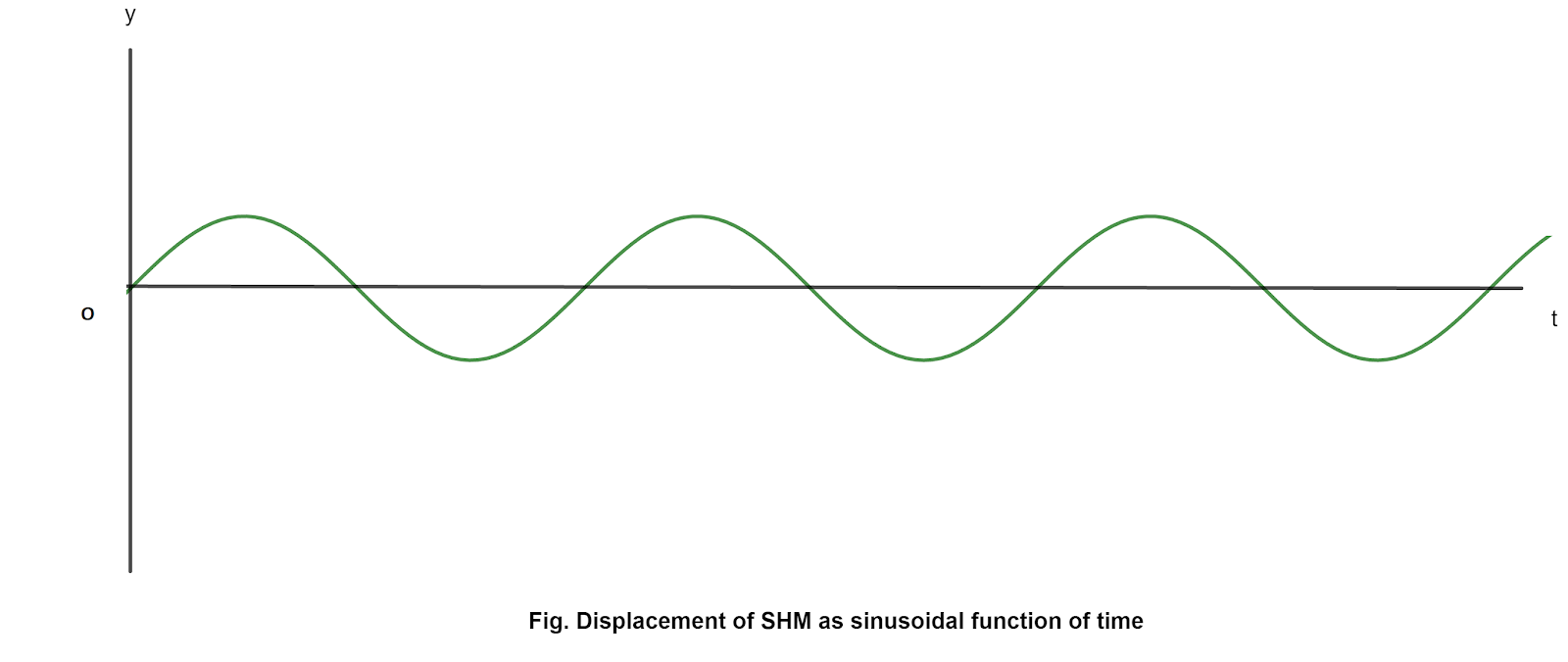
The displacement equation for a SHM is periodic and sinusoidal function of a time. i.e., \[y=rsin\omega t\]
Here, y is the displacement of the body in SHM at time t , r is its amplitude and \(\omega\) is its angular frequency.Velocity: Velocity is the time rate of change of displacement. i.e., \[\begin{align*} v&=\frac{dy}{dt}\\ &=\frac{d{rsin{\omega}t}}{dt}\\ &=r\frac{sin{\omega}t}{dt}\\ &=r\omega cos{{\omega}t}\\ \therefore v&=r{\omega} cos{{\omega}t} \end{align*}\] From this, \(v=r\omega \sqrt{1-sin^2\omega t}=rw\sqrt{1-\frac{y^2}{r^2}}=\omega \sqrt{r^2-y^2}\) From this equation, we see that the velocity is not uniform.
- When y = 0, \(v_{max}=\omega r\): velocity is maximum at mean position.
- When y = r, v = 0 : velocity is zero (minimum) at extreme positions.
Acceleration : Acceleration is the time rate of change of velocity. i.e., \[\begin{align*} a&=\frac{dv}{dt}\\ &=\frac{d(r\omega cos\omega t)}{dt}\\ &=r\omega \frac{d cos\omega t}{dt}\\ &=r\omega (-\omega sin\omega t)\\ &=-{\omega}^2 \times r sin\omega t\\ \therefore a&=-{\omega}^2 y \end{align*}\]
- When y = 0, \(a_{min}\)=0 : acceleration is minimum at mean position.
- When y = r, \(a_{max}=-{\omega}^2r\) : acceleration is maxmimum at extreme positions.
Amplitude : Amplitude is the maximum displacement of the particle from mean position. For \(sin\omega t=1\) in \(y = r sin\omega t\), the displacement becomes maximum. Thus, \[\text{amplitude}=y_{max}=r\]
Time period : Time period is defined as the time taken by the particle to complete one oscillation in SHM. i.e., \[T=2\pi \sqrt{\frac{y}{a}}\]
Frequency : Frequency is defined as the number of oscillations completed in one second. i.e., \[f=\frac{1}{T}=\frac{1}{2\pi} \sqrt{\frac{a}{y}}\]
Phase : The quantity \(\omega t\) is called the phase. It determines the status of the particle in simple harmonic motion.
If the phase is zero at a certain instant, \[y=r sin\omega t=rsin0=0\] and \[v=r\omega cos\omega t=r \omega\] This means that the particle is crossing the mean position and is going towards the positive direction.
If the phase is \(\frac{\pi}{2}\), we get \(y=r\) and \(v=0\) so that the particle is at the positive extreme position.
An increase of \(2\pi\) brings the particle to the same status in the motion. Phase of motion is the state of motion of the particle executing SHM. The status of the particle at different phases is shown in figure below.
A particle executing simple harmonic motion has angular frequency 6.28 /s and amplitude 10 cm. Find (a) the time period, (b) the maximum speed,
(c) the maximum acceleration, (d) the speed when the displacement is 6 cm from the mean position, (e) the speed at \(t=\frac{1}{6}\) s.
Here, \(\omega\) = 6.28 /s , r = 10 cm = 0.1 m , T = ?, \(v_{max}\) = ?, \(a_{max}\) = ?, v = ? when y = 6 cm = 0.06 m, v = ? when \(t=\frac{1}{6}\)
(a) Time period = \(\frac{2\pi}{\omega}\) = \(\frac{2\pi}{6.28}\) s = 1 s
(b) \(v_{max}\) = \(r \omega\) = \(0.1 \times 6.28\) = 0.628 m/s
(c) \(a_{max}\) = \(r {\omega}^2\) = \(0.1 \times (6.28)^2\) = 4 m/s\(^2\)
(d) \(v=\omega \sqrt{r^2-y^2}\) = \( 6.28 \sqrt{0.1^2-0.06^2}\) = 0.502 m/s
(e) At t = 0, the velocity is maximum, i.e., the particle is at an extreme. The equation for displacement may be written as,
\[y=rsin\omega t\]
The velocity is \(v=r\omega cos\omega t\).
At \(t=\frac{1}{6}\) s, \(v=0.1 \times 6.28 \times cos(\frac{6.28}{6}) = 0.627\) m/s
Simple Pendulum
A simple pendulum is a heavy point mass object suspended by an inextensible, weightless and flexible string from a rigid support which is free to oscillate in a vertical plane.
The position of the bob at any time can be described by the angle \(\theta\) between the string and the vertical. Let us see whether the motion of simple pendulum is simple harmonic or not and find out its time period of oscillation.
When the bob is displaced from its mean position, it oscillates along the path CAB in the vertical plane and at an instant, let the angular displacement be \(\theta\). The force acting on the bob at B are,
- Weight mg of the bob acting vertically downward,
- Tension T in the string along its length towards the point of suspension.
\[\therefore F=-mgsin\theta ... (i) \] Here, negative sign is due to the fact that the force is restoring in nature; it acts opposite to the displacement of the body.
If a be the acceleration of the bob, then \[F=ma=-mgsin\theta\] From this, \[a=-gsin\theta ... (ii)\] For small angular displacement \(\theta\), \(sin\theta \approx \theta=\frac{y}{l}\) where y is the displacement of bob from the mean position.
With this, equation (ii) becomes,
\[a=-g\left(\frac{y}{l}\right)=-\left(\frac{g}{l}\right) y ... (iii)\] For a given pendulum at a given place \(\frac{g}{l}\) is a constant and thus \(a\propto y\). Since, acceleration is directly proportional to the displacement from the mean position, it is the characteristic of SHM. So, simple pendulum executes simple harmonic motion .
Time period of a simple pendulum
Comparing equation (iii) with the standard equation i.e., \(a=-{\omega}^2y\), we get, \[-{\omega}^2=-\frac{g}{l}\] So, \[\omega=\frac{g}{l}\] So, the period of oscillation , \(T=\frac{2\pi}{\omega}\), so \[\begin{align*} \frac{2\pi}{T}&=\sqrt{\frac{g}{l}}\\ T&=2\pi \sqrt{\frac{l}{g}} ... (iv) \end{align*} \]Second's Pendulum
A simple pendulum whose time period is 2 seconds is called second's pendulum i.e., T = 2 s.
A simple pendulum has a period of 4.2 second, when the pendulum is shortened by 1 m the period
is 3.7 second. From these measurements, calculate the acceleration of free fall and the original length of the pendulum.
Here,
initial period of simple pendulum, T= 4.2 s,
initial length of simple pendulum l = ?,
final length of pendulum, l'=l-1 ,
final time period of pendulum, T'= ?,
acceleration of free fall, g= ?
Now,
\[\begin{align}
T&=2\pi \sqrt{\frac{l}{g}} \nonumber \\
4.2&=2\pi \sqrt{\frac{l}{g}} ... (i)
\end{align}\]
Then,
\[\begin{align}
T'&=2\pi \sqrt{\frac{l'}{g}} \nonumber \\
3.7&=2\pi \sqrt{\frac{l-1}{g}} ... (ii)
\end{align}\]
From these expressions,
Dividing eqn(ii) by eqn(i),
\[\begin{align*}
\frac{3.7}{4.2}&=\frac{l-1}{l}\\
\left(\frac{3.7}{4.2}\right)^2&=\frac{l-1}{l}\\
1-\frac{1}{l}&=\frac{1369}{1764}\\
\frac{1}{l}&=1-\frac{1369}{1764}\\
\frac{1}{l}&=\frac{395}{1764}\\
\therefore l&=4.47 \hspace{0.1cm} \text{m}
\end{align*}\]
To calculate g,
Using eqn (i),
\[\begin{align*}
4.2&=2\pi \sqrt{\frac{l}{g}}\\
\frac{4.2}{2\pi}&=\sqrt{\frac{4.47}{g}}\\
g&=10 \hspace{0.1cm} m/s^2
\end{align*}\]
Oscillation of a loaded spring
Vibration of particle in Horizontal spring
Suppose that one end of the spring S of negligible mass is attached to a smooth object A, and that A and S are laid on a horizontal smooth table as in figure. If the free end of S is
attached to the table and A is pulled slightly and then released. The system then vibrates with SHM. The mean position or the centre of
oscillation O is the position of A at the end of the spring corresponding to its natural length (i.e., when the spring is neither compressed nor extended).
If F be the restoring force set up in the spring on extension through l , then from Hooke's law,
\[\begin{align*}
F&\propto l\\
F&=-kl ... (i)
\end{align*}\]
Here, k is a force constant or spring constant. Negative sign shows that the restoring force acts opposite to the displacement of the body.
If m is the mass of A and a be its acceleration, then,
\[F=ma ... (ii)\]
From (i) and (ii),
\[\begin{align*}
ma&=-kl\\
a&=-\frac{k}{m} l\\
&=-{\omega}^2 l
\end{align*}\]
Here, \({\omega}^2=\frac{k}{m}\) is a constant. So, acceleration is directly proportional to the displacement and is directed towards the mean position. It is the characteristic of SHM. So,
the motion of a horizontal mass - spring system is simple harmonic motion.
Time period
We have, \({\omega}^2=\frac{k}{m}\) with \(\omega\) being the angular velocity. Then, the time period of oscillation is, \[\begin{align*} T&=\frac{2\pi}{\omega}\\ &=2\pi \sqrt{\frac{m}{k}} \end{align*}\]
Vibration of particle in vertical spring (Oscillation of mass suspended from helical spring)
Consider the spring of force constant k suspended from the fixed rigid point as in figure. When a mass m is placed on it, the spring stretches to O by a length l given by,
\[mg=-kl\]
Here, mg is the restoring force on the spring.
If the mass is pulled down a little and then released, it vibrates up - and - down above and below O. Suppose at an instant that B is at a distance y below O. Then the restoring force of the spring is equal to,
\[-k(l+y)\].
Then, the effective restoring force which causes the oscillation is \(-k(l+y)-(-kl)\) and since effective force = ma ,
\[\begin{align*}
-kl-ky+kl&=ma\\
-ky&=ma\\
a&=-\frac{k}{m} y\\
a&=-{\omega}^2y\\
\therefore a&\propto y
\end{align*}\]
Here, \({\omega}^2=\frac{k}{m}\) is a constant. Since, accleration is directly proportional to the displacement and is directed towards the mean position. It is the characteristic of SHM and thus oscillation of particle in
vertical spring is simple harmonic motion.
Time period
Time period T is given by, \[T=\frac{2\pi}{\omega}=2\pi \sqrt{\frac{m}{k}}\]
A block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are
0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.
Here, mass, m = 5 kg; amplitude, x = 0.1 m; time period, T = 3.14 s
The angular frequency, \[\omega=\frac{2\pi}{T}=2 s^{-1}\]
The spring constant, \[k=m{\omega}^2=5\times 4=20 \hspace{0.1cm} Nm^{-1}\]
Maximum force , \[=kx=20\times 0.1=2 \hspace{0.1cm} N\]
Energy in SHM
Simple harmonic motion is defined by the equation, \[F=-ky \because a=-{\omega}^2y\]
where y is the displacement, r is the amplitude and \(\omega\) is the angular velocity.
The work done by the force F during a displacement y to y+dy is, \[dW=Fdy=-kydy\]
The work done in a displacement from y=0 to is, \[W=\int^y_0 (-ky)dy=-\frac{1}{2}ky^2\]
This work done is stored in the form of potential energy of the system. i.e., \[E_p=\frac{1}{2}ky^2=\frac{1}{2}m{\omega}^2y^2 ... (i)\]
Kinetic energy of the particle with velocity v is given by, \[E_k=\frac{1}{2}mv^2=\frac{1}{2}m(\omega \sqrt{r^2-y^2})^2=\frac{1}{2}m{\omega}^2(r^2-y^2) ... (ii)\]
Total energy of the particle at any point is,
\[\begin{align*}
E&=E_p+E_k\\
&=\frac{1}{2}m{\omega}^2y^2+\frac{1}{2}m{\omega}^2(r^2-y^2)\\
&=\frac{1}{2}m{\omega}^2r^2
\end{align*}\]
Since, m , \(\omega\) and r are constants, the total energy remains constant for a particle executing SHM.
- When the paricle is at the mean position, y=0 ;
\[E_p=\frac{1}{2}m{\omega}^2 \times 0=0\] and, \[E_k=\frac{1}{2}m {\omega}^2 r^2-\frac{1}{2}m{\omega}^2(0)^2=\frac{1}{2}m{\omega}^2r^2\] In this case, the total energy is equal to the maximum value of K.E. - When the particle is at the extreme position, y = r ,
\[E_p=\frac{1}{2} m {\omega}^2 r^2\] and, \[E_k=\frac{1}{2}m{\omega}^2r^2-\frac{1}{2}m{\omega}^2r^2=0\] So, the total energy is equal to the maximum value of P.E.
A block has mass \(2.72\times10^5\) kg and is designed to oscillate at frequency 10.0 Hz and with amplitude 20 cm. (a) What is the total mechanical
energy E of the spring - block system? (b) What is the block's speed as it passes through the equilibrium point?
Here, mass, m = \(2.72\times 10^5\) kg, frequency, f = 10 Hz, amplitude, r = 0.2 m
(a) Total mechanical energy, \(E=E_p+E_k\)
\[\begin{align*}
E_p&=\frac{1}{2}m{\omega}^2 y^2\\
&=\frac{1}{2}\times 2.72\times 10^5 \times (2\pi \times 10)^2\times (0.2)^2 \because y=r\hspace{0.1cm} \text{at extreme position}\\
&=2.147 \times 10^7 \hspace{0.1cm} J
\end{align*}\]
And, \[\begin{align*}
E_k&=\frac{1}{2}m{\omega}^2 r^2-\frac{1}{2}m {\omega}^2y^2\\
&=\frac{1}{2}m{\omega}^2 r^2-\frac{1}{2}m{\omega}^2 r^2 \because y=r\hspace{0.1cm} \text{at extreme position}\\
&=0
\end{align*}\]
Thus, total mechanical energy is \(E_p+E_k=2.147 \times 10^7\) J.
Note that! The mechanical energy of the spring - block system is constant throghout the motion and thus we can evaluate E at any point during the motion.
(b) At equilibrium point, r = 0 and thus potential energy, \(E_p=\frac{1}{2}m{\omega}^2r^2=0\).So, total mechanical nergy is equal to the kinetic energy.i.e.,
\[\begin{align*}
2.147\times 10^7&=\frac{1}{2}mv^2\\
v^2&=\frac{2\times 2.147\times 10^7}{2.72\times 10^5}\\
v&=12.6 \hspace{0.1cm} m/s
\end{align*}\]
So, the speed of block when it passes through the equilibrium point is 12.6 m/s.
A steel strip, clamped at one end, vibrates with a frequency of 20 Hz and an amplitude of 5 mm at the free end, where a small mass of 2g
is positioned. Find (a) the velocity of the end when passing through the zero position, (b) the acceleration at maximum displacement, (c) the maximum kinetic and potential energy of the mass.
Here, mass, m = \(2\times 10^{-3}\), frequency, f = 20 Hz, amplitude , r = \(5\times 10^{-3}\)
(a) \(v=\omega sqrt{r^2-y^2}\). At zero position, y=0 and thus,
\[v=\omega r= 2\pi f r=2\pi \times 20 \times 0.005=0.628 \hspace{0.1cm} m/s\]
(b) \(a=-{\omega}^2y\). At maximum displacement, y=r and thus,
\[a=(2\pi f)^2 \times r=(2 \pi \times 20)^2\times 0.005=79 \hspace{0.1cm} m/s^2\]
(c) Maximum kinetic energy is, \[(E_k)_{max}=\frac{1}{2} m v^2=\frac{1}{2} \times 2\times 10^{-3}\times (0.628)^2=3.94\times 10^{-4}\hspace{0.1cm} J\]
Maximum potential energy is, \[(E_p)_{max}=(E_k)_{max}=3.94\times 10^{-4}\hspace{0.1cm} J\]
Damped oscillation
When dissipative forces such as friction or viscous force acts on a body executing SHM, the forces offer resistance to the motion. This resistive forces are called the damping forces. The damping force is a function of speed of the moving system and is directed opposite to the velocity. Energy is lost due to the negative work done by the damping force and the system comes to a halt in due course. This type of motion is called damped oscillation and the vibration is damped. The motion of a pendulum in a liquid, to and fro motion of a metallic strip in a magnetic field are examples of this type of oscillation.
Free oscillation
When a system or body capable of oscillating is given some initial displacement from its equilibrium position and left free, it begins to oscillate with its own natural frequency with constant amplitude. Then the oscillation of the body is called free oscillation. Oscillation of pendulum, tuning fork or string, person swinging in a swing,etc. are examples of this type of motion.
Forced vibration and Resonant vibration
If a body is set in vibration by an external periodic force, then the body is set to be in forced oscillation . If the frequency of the periodic force is equal to the natural frequency of the vibrating body, the amplitude of vibration increases at each step and becomes very large. Such vibration is called resonant vibrations and the phenomena is called the resonance.
Note! All mechanical structures have one or more natural angular frequencies. So, when the external driving force or periodic force matches one of this natural frequencies, the resulting oscillation (resonant) may rupture it. Thus, aircraft designers must make sure that none of the natural frequencies at which wing can oscillate matches the frequency of the engines in the flight. The displacement y of a mass vibrating with simple harmonic motion is given by \(y=20 sin 10\pi t\), where y
is in millimetres and t is in seconds. What is (i) the amplitude, (ii) the period, (iii) the velocity at t=0?
Comparing \(y=20sin10\pi t\) with the standard equation of SHM i.e., \(y=rsin{\omega}t\), we get,
r = 0.02 m.
From \[\begin{align*}
\omega&=10\pi\\
2\pi f&=10\pi\\
f&=5 \hspace{0.1cm} \text{Hz}\\
\therefore T&=\frac{1}{f}=0.2 \hspace{0.1cm} s
\end{align*}\]
Velocity is, \[v=r\omega cos\omega t=0.02\times 10\pi \times 1\because t=0\]
\[\therefore v= 0.628 \hspace{0.1cm}m/s\]
Click on Periodic motion questions to find the important questions.
Click on Periodic motion solutions to find the solutions to short questions and numerical problems.







This comment has been removed by a blog administrator.
ReplyDelete