Surface tension (Fluid statics) | Complete notes | Important questions | Short questions and Numerical problem solutions | Class 12 (Physics) | Physics in Depth
Intermolecular forces : Origin and its types
Forces that exists between molecules either of same types or different types within the molecular range are called the intermolecular forces .
Intermolecular forces arises from two main causes:
- Potential energy of the molecules (due to the interactions between surrounding molecules-principally electrical in origin).
- Thermal energy of the molecules ( i.e., kinetic energy of the molecules): Depends on the substance concerned.
Energy of liquid surface : Molecular theory
The properties of a surface are quite often markedly different from the properties of the bulk material.Consider the figure:
- Molecule A is surrounded by equal number of molecules on all sides. This is seen by drawing a sphere around A. The average distance apart of molecules is such that the attractive forces balances the repulsive forces. Thus the average intermolecular force between A and the surrounding molecule is 0. \[\Sigma F=0\]
- Molecules such as C or B are in the surface of liquid. There are very few molecules on the vapour side above C or B compared with the liquid below.
- If C is displaced very slightly upward, a resultant attractive force F on C due to the large number of molecules below C, now has to be overcomed.
- It follows that if all the molecules in the surface were removed to infinity, a definite amount of work would be needed. Cosequently molecules in the surface have potential energy.
- A molecule in the bulk of the liquid forms bonds with more neighbours than one in the surface.
- This bonds must be broken ,i.e., work must be done to bring a molecule into the surface.
- Thus, molecules in the surface of the liquid have more potential energy than those in the bulk.
Surface Tension
Imagine a line AB drawn on the surface of a liquid (as in fig.). AB divides the surface in two parts, surface on one side and the surface on the other side of the line.Two parts of the
surface pulls each other with a force proportional to the length of the line AB. These forces are perpendicular to the length and tangential to the surface. Thus, surface of liquid behaves
like a stretched rubber sheet.Surface tension T of a liquid is the force F per unit length l acting on either side of a line drawn in the
liquid surface in equillibrium the direction of force being tangential to the surface and perpendicular to the line.
\[ T=\frac{F}{l}\]
The S.I. unit of surface tension is Nm\(^{-1}\).
Dimension of surface tension=\(\frac{\text{dimension of force}}{\text{dimension of length}}=\frac{[MLT^{-2}]}{[L]}=[MT^{-2}]\)
Surface area and shape of drop
Surface area
Consider the fig. below. Surface tension forces on both sides of thread counterbalance each other.
Shape of drop
For a stable equilibrium, minimum potential energy of system is required. Thus, under surface tension forces- minimum number of molecules in the liquid surface. For a given volume of liquid, spherical shape has minimum surface area. Due to this reason, small drop of liquid is spherical in shape. Larger drops are flat because the gravitational force is relatively greater and the shape of drop must agree with the principle that the sum of gravitational P.E. and the surface energy is minimum and thus C.G. comes down as low as possible.
A light wire AB of length 10 cm can slide on a vertical frame as shown in figure below. There is a film of soap solution trapped between
the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soap solution=25 dyne cm\(^{-1}\).
Take g=10 m/s\(^2\).
Since soap film will be formed on both the sides and each film is in contact with the wire along a distance of 10 cm, the force exerted by the film on the wire is, \[\begin{align*} &=2\times 10\times 25\\ &=500\\ &=5\times 10^{-3} \hspace{0.1cm} \text{N} \end{align*}\] This force acts vertically upward and should be balanced by the load. Hence the load to be suspended is \(5\times 10^{-3} \hspace{0.1cm} \text{N}\).The mass of the load is then, \(\frac{5\times 10^{-3}}{10}=5\times 10^{-4} \hspace{0.1cm} \text{kg}\).
Surface Energy
Extra energy that a surface layer has is called the surface energy. Consider a rectangular frame with a sliding wire on its arm dipped on a soap solution and taken out.
Find the work done required to break up a radius 5\(\times10^{-3}\) m into eight drops of water, assuming isothermal condition.
Given,
radius of original drop, \(R=5\times 10^{-3}\) m, number of final drops, \(n=8\), work done =?
Let r be the radius of each broken droplet.
The volume of the original drop is,
\[V=\frac{4}{3} \pi R^3\]
The volume is also,
\[V=8\times \frac{4}{3} \pi r^3\]
Thus, \[8r^3=R^3\]
\[r=\frac{R}{2}\]
The surface area of the original drop is \(A_1=4\pi R^2\) and that of 8 drops is,
\(A_2=8 \times 4\pi r^2=8\times 4 \pi \frac{R^2}{4}=8\pi R^2\)
The increase in area is ,
\[\Delta A=A_2-A_1=4 \pi R^2\]
The work done required to break the drops is equal to the change in surface energy and thus,
\[\begin{align*}
\sigma&=\Delta A \times T\\
&=4 \pi (5 \times 10^{-3})^2 \times 7\times 10^{-3}\\
&=2.2 \times 10^{-6} \hspace{0.1cm} \text{J}\\
\end{align*}\]
Excess pressure on curved surface of a liquid
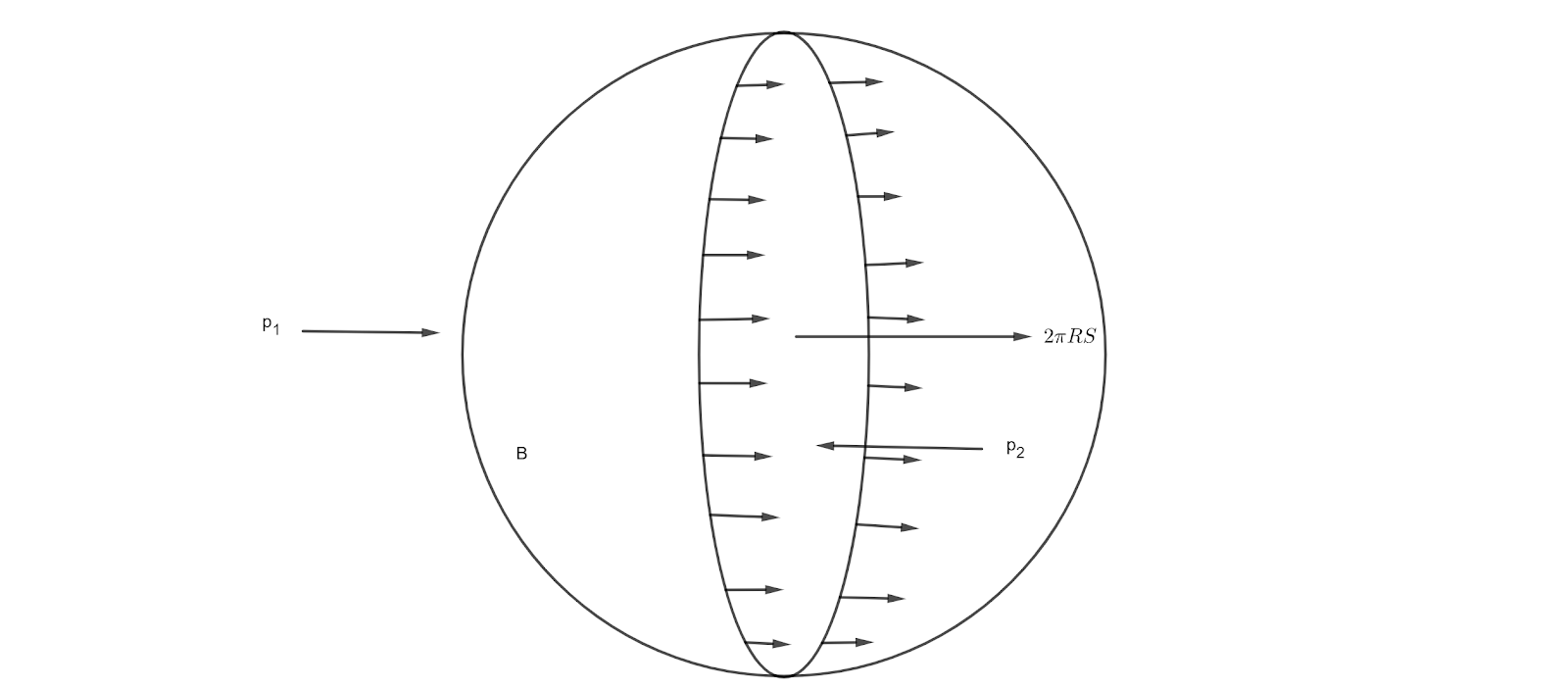
Considering the equilibrium of one half B of the liquid drop;
Surface tension force on B=\(2\pi R T\) where R is the radius of circular cross-section,
force on B due to external pressure \(p_1=\pi R^2 p_1 \hspace{0.1cm}\because \text{pressure}=\frac{\text{force}}{\text{area}}\) and
force on B due to internal pressure \(p_2\) inside the drop = \(\pi R^2 p_2\). So, equation (i) becomes, \[\begin{align*} \pi R^2 p_2&=2\pi R T+\pi R^2 p_1\\ R(p_2-p_1)&=2T\\ p_2-p_1&=\frac{2T}{R} \end{align*}\] The pressure inside the liquid surface is greater than the pressure outside the surface by an amount \(\frac{2T}{R}\).
Excess pressure in soap bubble
Since, a soap bubble has two liquid surfaces in contact with air, one inside the bubble and the other outside the bubble. \[p_2-p_1=\frac{4T}{R}\]
Contact angle
When a liquid surface touches a solid surface, the shape of the liquid surface near the contact is generally curved. When a glass plate is immersed in water, the surface near the plate
becomes concave as if the water is pulled up by the plate. On the other hand, if a glass plate is immersed in mercury, the surface is depressed (i.e., convex ) near the plate.
The angle between the tangent planes at the solid surface and the liquid surface at the contact is called the contact angle. In this the tangent plane to the solid surface is to be drawn
towards the liquid and the tangent plane is to be drawn away from the solid. Figure below shows the contact angle.
Why does the liquid surface bend near the contact with the solid?
- P, the adhesive force between solid and liquid in contact. ( It is perpendicular to the solid and is into the solid.)
- Q, the cohesive force between the liquid molecules.( Its direction and magnitude depends on the shape of the liquid surface).
- W, the weight of the part considered.
The direction of the resultant of P , Q and W decides the shape of the surface near the contact. The liquid rests in such a way that the surface is perpendicular to this resultant. If the resultant passes through the solid, the surface is concave upward and the liquid rises along the solid. If the resultant passes through the liquid, the surface is convex upward and the liquid is depressed near the solid.
Measurement of surface tension by capillary rise method
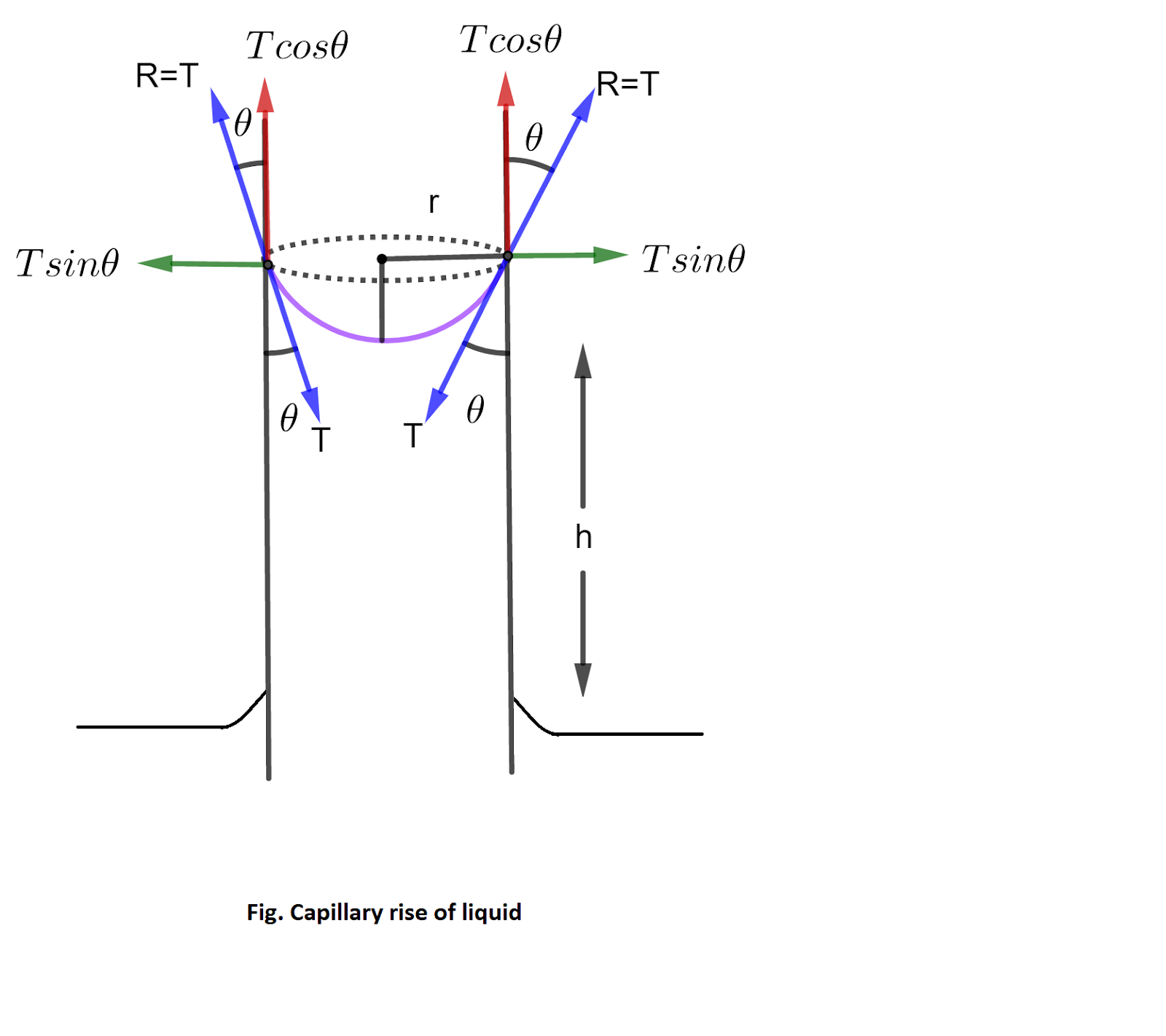
Consider a capillary tube of radius r dipped into a liquid which forms the concave meniscus as in figure. Let \(\theta\) be the contact angle, h be the height upto
which the liquid rises, \(\rho\) be the density of the liquid and T be the surface tension of liquid.
The surface tension forces T acts along the tangent at the point of contact and weight of liquid column is acting downward. From Newton's third law of motion,
- Tcos\(\theta\) along the vertical and
- Tsin\(\theta\) along the horizontal
So, total upward force, \[F=Tcos\theta \times 2\pi r\] Volume of the liquid in the tube above the free surface of liquid is,
\[\begin{align*} V&=\pi r^2 h + \pi r^2 r -\frac{1}{2} \left(\frac{4}{3} \pi r^3\right)\\ &=\pi r^2 h + \pi r^3 - \frac{2}{3} \pi r^3\\ &=\pi r^2 h+\frac{1}{3}\pi r^3\\ &=\pi r^2 \left(h+\frac{r}{3}\right) \end{align*}\] Weight of liquid column is, \[W=\rho V g = \rho \pi r^2 \left(h+\frac{r}{3}\right)g\] For equilibrium, \[\begin{align*} \text{Total upward force}&=W\\ Tcos\theta \times 2\pi r &=\rho \pi r^2\left(h+\frac{r}{3}\right)g\\ T&=\frac{\rho r \left(h+\frac{r}{3}\right)g}{2cos\theta}\\ \end{align*}\] When the tube is of very fine bore, \(\frac{r}{3}\) can be neglected compared to h and thus above expression becomes, \[T=\frac{\rho r h g}{2cos\theta}\] This is the expression for the surface tension of the liquid. From this expression , \(h=\frac{2Tcos\theta}{r\rho g}\). So, we can conclude the following:
- If angle of contact \(\theta \lt 90^\circ\), then \(cos\theta=+ve\) .So, h is +ve and the liquid rises in the capillary tube.
- If angle of contact \(\theta \gt 90^\circ\), then \(cos\theta=-ve\). So, h is -ve and the liquid falls in the capillary tube.
Angle of contact of mercury with glass is \(135^\circ\). A narrow tube of glass having diameter 2 mm is dipped in a beaker containinng mercury
. By what height does the mercury go down in the tube relative to the level of mercury outside?
Here,
\(\theta\)=\(135^\circ\), radius , r = \(\frac{d}{2}\) = 1 mm = 0.001 m, surface tension of mercury, T = 0.5 Nm\(^{-1}\), density of mercury, \(\rho\) = 13600 Kgm\(^{-3}\)
Now,
\[\begin{align*}
h&=\frac{2T cos\theta}{r\rho g}\\
&=\frac{2 \times 0.5 \times cos135^\circ}{0.001\times 13600 \times 10}\\
&=-5.19 \times 10^{-3} \hspace{0.1cm} m
\end{align*}\]
So, the mercury goes down by 5.19 mm relative to the mercury level outside.
Describe the rise of liquid in a tube of insufficient length.
We have, \[h=\frac{2Tcos\theta}{r \rho g}\] For tube of sufficient length as in first figure,
We see that, \[r=Rcos\theta\] Putting this in first expression, \[h=\frac{2Tcos\theta}{Rcos\theta \rho g}=\frac{2T}{R\rho g}\] So, for a given liquid, \[hR=\frac{2T}{\rho g}=\text{constant}\] Now, consider the case when the tube is of insufficient height h' ie., h' < h . Let, the radius of curvature in this case be R' and since, \[h'R'=hR= \text{constant}\] Also, h'>h, it follows that, \[R' \gt R\] So, there is an increase in radius of curvature of the liquid meniscus and the liquid spreads in the material of the tube without overflowing.
Click on Surface tension questions to find the important questions frequently asked in National Examinations board (NEB).
Click on Surface tension solutions to find the solutions to short and numerical problem solutions.
""
ReplyDeleteThis equipment has been recognized as cost-effective and specially designed for restorative and preventive purposes in maintenance techniques for roads, most traffic points, airports, taxiways, and highways. It is a mixture of polymer-modified asphalt emulsion, mineral aggregate, mineral filler, water, and other additives.